みなさん、こんにちは。受験ドクター算数科のA.K講師です。

前回のブログでは、以下のような損益算＋特殊算が絡む割合のオリジナル問題を出しましたね。憶えていますでしょうか？

【解説】
(1)仕入れにかかった総額が等しいので、個数の逆比で150:100=3:2です。
(2)ここからが今日の内容です。定価について聞かれているので、ヒントになることがどこに書かれているかというと…

「また、どちらの商品も60円の利益をつけて定価を決めたところ、A商品とB商品の定価の比は
1個あたりで4：3となったそうです。」

ここですね！

① (1)から商品の元値の比が出た
② 商品はA・Bと2種類ある
③ さらに定価の比も書いてある

上記3つの条件から、これは倍数算であることが分かります。各々の商品について式にすると以下のようになります。

A　③+60=
B　②+60=

ここから、両者の差を取ると①= となり、比を○にそろえると④-③=①=60となるので1個あたりのB商品の定価は60×3=180円とわかります。なお、A商品の定価は60×4=240円です。

(3)これがちょっと難問だったかもしれません。亀井商店では、B商品について1個あたりの値段が定価である180円、180-40=140円、さらには180-80=100円と3種類にわかれてしまっており複雑な商売をしています。一方、A商店は定価で全て売り切ったので、売上総額は240×100個=24000円です。両商店で売上総額が同じなので、亀井商店の売上総額も24000円。
売り方は180、140、100円と3種類・売った個数の合計は仕入れた個数と同じで150個・売上総額は24000円…このことから、まずはつるかめ算であることが分かりますね！
ただ、3種類あるので何とかならないものか…と問題文を見てみると、

「定価の40円引きしたものと80円引きしたものはそれぞれ同じ個数ずつ売れた」

とあるじゃないですか！
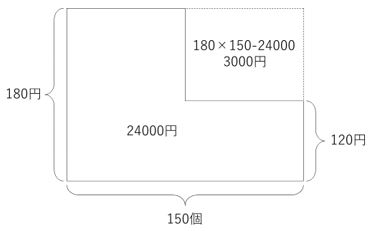
140円で売ったものと100円で売ったものの個数が等しいので、値段の平均をとると(140+100)÷2=120円で売ったことと同じです。あとは下のように2段のつるかめ算を解くだけ…

3000÷(180-120)=50個となりますが、これは140円で売ったものと100円で売ったものの個数の合計なので答えは50÷2=25個となるわけです！

いかがでしたでしょうか。
それでは、この辺で今日の内容の総括に移りたいと思います。

～本日のまとめ～
・問題文の条件を一つ一つ整理し、吟味することで何算を使うのかをまずは考える。
・文章の長い問題だったとしても、そこには必ずヒントとなることが記されているので、計算できるものから計算を進めて次を考えていくようにする。

今回はここまでといたしましょう。
次回は、秋も深まってきてそろそろ入試の足音が近づいてきています…入試対策ということで、どこかの学校の問題を一緒に考えていきたいと思います！

ではまた、お会いしましょう♪