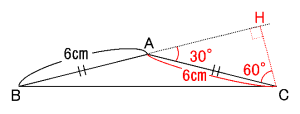みなさん、こんにちは。
受験ドクター算数科の江田です。

突然ですが問題です。

今日は１１月２９日。
何の日でしょう？

えぇ、
想像に難くないでしょう。
「いい肉の日」です♪

ところがどっこい、調べてみたら
「いい服の日」
でもあるんですって。

言われてみれば、
確かにそうとも読めますね。

うーむ、こりゃあ今夜は
いい服着て、いい肉食べるしかないですな♪

さて、
今回も余談はこれくらいにして…

前回のブログで

「30°，60°，90°の直角三角形はちょ～怪しい！！」
というお話をいたしました。

今回は
その注目ポイントを利用した
実戦演習です。

さっそくいってみよ～♪

【問題１】
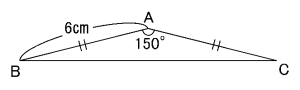
下の図の二等辺三角形ABCの面積は何㎠ですか。

考え中…

考え中…

さぁ、いかがでしょうか。

頂角（と言われる部分）が150°の二等辺三角形です。
前回のブログでは頂角が30°の二等辺三角形でしたね。

前回と同じように
どの辺を底辺として見るか
を考えましょう。

唯一具体的に長さがわかっている
辺ABを底辺として見ると
高さは下図のCHとなります。

もうお気づきの方も多いかもしれません。

そうです。
三角形ACHが例の
「30°，60°，90°の直角三角形」
になっているんですね。

ということで、高さCHの長さはACの長さの半分で
6÷2＝3 （㎝）
とわかり、求める二等辺三角形ABCの面積は
6×3÷2＝9 （㎠）
となります。

頂角の150°という数値が
この問題を解くカギとなるわけですね。

それではもう１問。

【問題２】
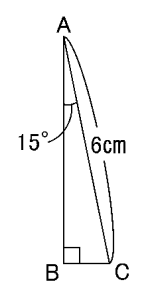
下の図の直角三角形ABCの面積は何㎠ですか。

考え中…

考え中…

さて、これはいかがでしょうか。
これも素直に
唯一具体的に長さがわかっている
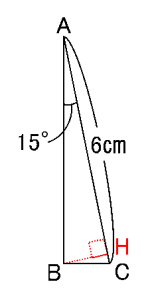
辺ACを底辺として見ると
高さは下図のBHとなります。

うーん…
「超怪しい三角形」はいずこに…？

そうなんです。
これじゃ「30°，60°，90°の直角三角形」が現れないんです。

ここでポイントとなるのはもちろん15°という角度。
これを用いて見慣れた怪しい数値にしたい。

そうです。
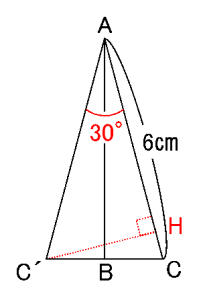
下図のように、
この三角形を２つ組み合わせて30°を作り出せばよいのです。

すると
まさに前回のブログで登場した
頂角が30°の二等辺三角形になります。

三角形AC´Hが「超怪しい三角形」 となり、
C´Hの長さが
6÷2＝3 （㎝）
とわかりますね。
よって三角形AC´Cの面積が
6×3÷2＝9 （㎠）
で、三角形ABCはこの半分ですから
9÷2＝4.5 （㎠）
と求まるわけです。

ちなみに、この問題は
もとの三角形ABCを下図のように2つ組み合わせ、

【問題１】と全く同じ
頂角が150°の二等辺三角形
として考えていくこともできますね。

そう考えて
【問題１】の半分！
と思った方もいらっしゃったかも知れません♪^^

どちらの考え方にせよ最大のポイントは
「与えられた数値を利用して、いかにして“超怪しい三角形”を作り出すか」
です。

今回のブログでは
その基本ともいえる典型題をご紹介しましたが、
実際の入試問題では
そう簡単に見つけられる問題ばかりではありません。

いつ出題されてもいいように
常に頭の片隅に「超怪しい三角形」を置いておく
ことが大切です。

これをご覧いただいた皆さんのお子様に
是非このことを伝えてください♪

それではまた次回お会いしましょう！！