こんにちは、算数を担当しております佐々木です。

本日は、「ちょっとずつずれちゃう」お話を致します。

「数の性質」を勉強するときに、必ず出てくる
「4で割ると3余り、6で割ると1余る2けたの整数で最大となる数を求めなさい。」
という類の問題です。

これは、まず、書き出すことがポイントです。
しかし、全部書き出す必要はありません。

「4で割ると3余る」数は、3，7，11，15，19・・・
「6で割ると1余る」数は、1，7，13，19，25・・・

両方に等しい数の中で、一番小さい数は、「7」です。
その後、どこに出てくるかというと、「19」ですね。19の次が、31、43、55、・・・と続きます。

19―7＝12

この12の意味はなんでしょうか。

ちゃんと意味があります。

これは、4ずつ増える数字と、6ずつ増える数字の、共通する整数。
つまり、4と6の最小公倍数。

だから、初めにでてきた、「７」を求めることができれば、
そのあとは、ずっと12増えるごとにでてきます。

これを図に表すと、

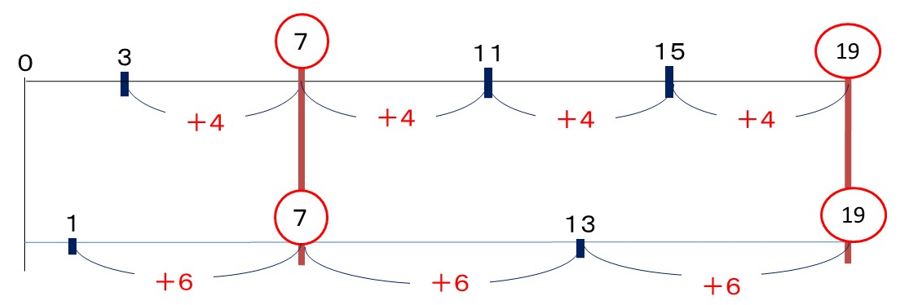
「７」がはじめに出てくると、次は、
４と６の最小公倍数ごとに出てくるので、12をどんどん足していけばいいのです。

2けたで一番大きい数字は、100÷12＝8・・・4
12×8＝96　⑦ずれているので、96＋⑦＝103
12×7＝84　⑦ずれているので、84＋⑦＝91

問題の条件「2けた」にあうのは、「９１」ですね。

しかし、指導していて一番多い誤答は、

12の倍数であることをそもそも忘れて、
はじめに「７」が出てきたので、7ずつ足していく、というパターンです。

100÷7＝14・・・２
7×14＝98と答えにしてしまいます。

そうではなくて、

あくまでも、はじめにでてきた整数が「７」なだけで、
そのあとは、「4ずつ増えていく整数」と「6ずつ増えていく整数」の
ちょうど揃うところ＝最小公倍数ずつ増えるということに注意しましょう。

もちろん、最小公倍数「12」が基本ですので、
先程の図に「12」の倍数の線分図も入れてみます。
そうすると、

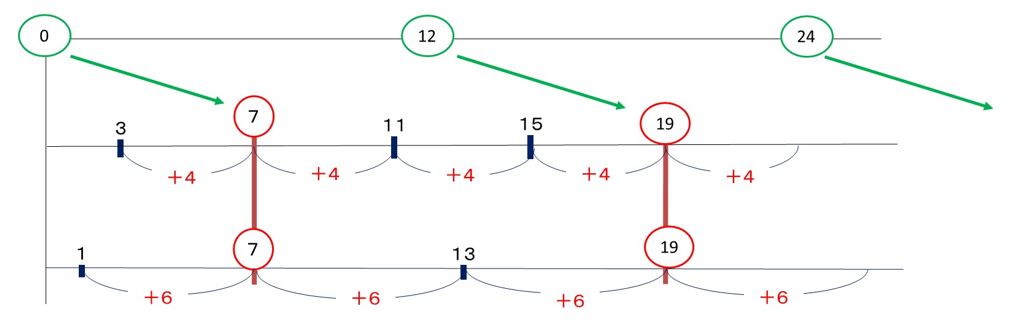
上図のようになります。
７、１９、３１、・・・と続く数字は、
実は、もとの12の倍数と7ずつずれているということがわかりますか。

「ちょっとずつずれてしまう」のです。

規則的に並んでいる整数というのは、どこかでルールが全く変わるということではなく、
何かルールがあり、それに則って、並んでいるのです。

一見、「4で割ると3余り」「6で割ると1余る」整数には共通な部分がないように
見えますが、実は、4と6に大きな意味があったのです。

そのルールを見抜くようにしましょう。

そして、

今日、私は、
電車を一本逃してしまい、10分ずつ遅れて、
都営浅草線⇒山手線⇒中央線と、乗り換えて吉祥寺に辿り着きました。
ちょっとずつずれてしまったのです。

やっぱり、電車って規則的に動いているんだなと痛感しました。

それでは、本日はこれまで。

ありがとうございました！