卒業生のみなさん、入試がおわってもうすぐ３か月がたとうとしていますが
いかがお過ごしでしょうか。桜とともに入学式を迎え、
もうすっかり中学校の生活にも慣れてきた頃でしょうか。
ドクターの先生たちは、君たちの今後のご活躍を心より応援しています。ということで、卒業してもドクターのブログを見に来てくださいね。

こんにちは。そして、はじめまして。　TS講師と申します。

今日は、対角線によって何枚の正方形が切断されますか？　という問題についてお話をしようと思います。問題をみれば、「あぁ～　これか～」とどこかで見たことがあるかもしれない有名な問題です。
こんな問題です。

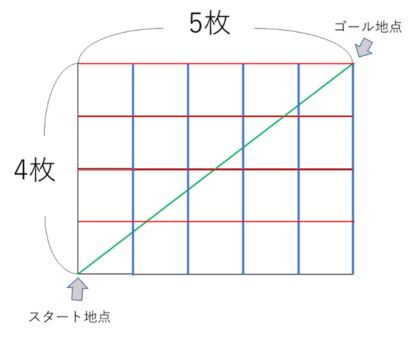
対角線によって何枚の正方形が切断されたでしょうか。

出発点からゴールの点まで対角線を引くと
青いの縦の壁を５枚通過しなければ横方向に進めないのでゴールできません。
こんどは、赤い横の壁を４枚通過しないと縦方向に進めないのでゴールできません。
では、縦と横、あわせて何枚の壁を通過したことになるでしょうか。

縦5枚　横４枚だから　合わせて9枚の壁を通過したことになりますね。

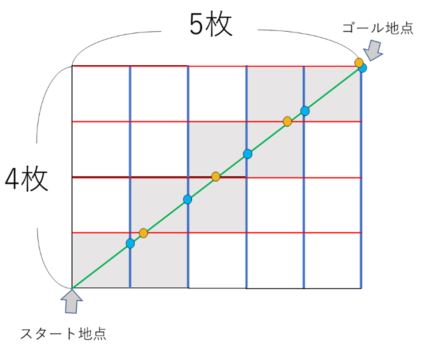
では、通過した地点に印をつけてみます。図を見てみましょう。
こんな感じなります。（下の図）

印は９個つきましたね。
でも、ゴール地点の点は2つの点が重なりますので、
点の箇所は８か所になります。
このゴール地点では、点が重なるので　“ひく１”　をするのです。

さて、対角線によって正方形は何枚切断されたことになるでしょう。

正方形８枚が切断されていますね。
よって、切断される正方形の枚数は、

ということがわかります。

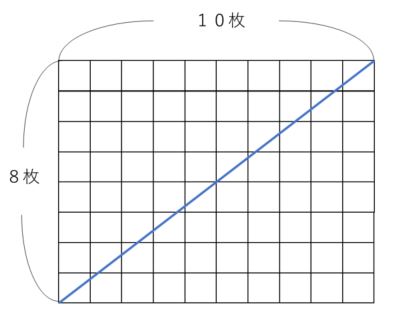
では、こんな問題にもチャレンジしてみましょう。

何枚の正方形が対角線によって切断されたかというと
８＋１０－１＝１７（枚）　と言ってしまいたくなりますよね。
でも答えは、１６枚です。
あれ？　　なんで？
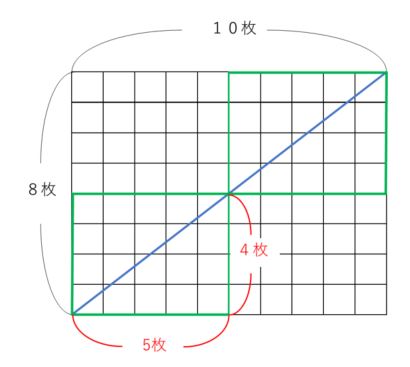
図をよく見ると、先ほどの縦４枚、横５枚の長方形が対角線上に２つ分あることがわかります。
ですから、８枚×２＝１６枚になるわけです。

縦の枚数と横の枚数が１以外の公約数をもたない枚数まで小さくして考えます。
縦の８枚、横の１０枚はそれぞれ
８＝４×２　　１０＝５×２　なので
縦４枚　横５枚に正方形を並べた長方形が対角線上に２個ある
というように考えればよいのです。

では、最後にもう１題考えてみましょう。

答えは出せましたか？

縦の枚数と横の枚数が１以外の公約数をもたない枚数まで小さくして考えます。
９１＝７×１３　　１５６＝１２×１３　なので
縦７枚　横１２枚に正方形を並べた長方形が対角線上に１３個分あるとわかります。
縦７枚　横１２枚に正方形を並べた長方形の対角線によって
切断させる正方形の枚数は
７＋１２－１＝１８枚　　となるので、
１８×１３＝２３４枚　です。

お話はこれでおしまいです。

では、みなさん　またお会いしましょう。