みなさん、こんにちは。受験ドクターの亀井章三です。

 

４月といえば新学期！受験勉強を終えた元受験生たちも

４月からは新中学１年生です。

新たな学校生活、友人、部活と楽しいことがいっぱい待っています。

 

でも、中学校に入ると勉強が難しくなるのも事実。

特に、算数は「数学」と名前を変え、皆様を待っています。

 

数学って難しそう…と思ってしまいますよね。

そんな数学の世界を今日は一足先にご紹介！

 

小学生でも使えて役立つ公式を一つ教えちゃいます。

これで算数も数学もバッチリ！

 

それではいってみよー！

 

 

＜○×○－□×□＞

そもそも因数分解って何？と思われますが、似たような言葉は

聞いたことがあるはず。

 

それは、「素因数分解」です。

 

素因数分解は、整数において素因数（素数と同じと考えてＯＫ）の積に

分解すること。

因数分解は、文字式を因数とよばれる一番単純な文字式の積に分解

すること

 

言葉で書くと難しいのですが、式にすると結構わかりやすいのです。

今日ご紹介する因数分解はこちら！

 

　○×○－□×□＝（○＋□）×（○－□）

 

平方数の差は、その数の和と差の積に等しい、というものです。

 

例えば、

 

３×３－２×２＝（３＋２）×（３－２）＝５×１＝５

５×５－３×３＝（５＋３）×（５－３）＝８×２＝１６

 

となります。

 

この因数分解を使えば、こんな計算も楽勝！

 

２０１７×２０１７－２０１６×２０１６＝

 

普通に計算すると、

２０１７×２０１７＝４０６８２８９

２０１６×２０１６＝４０６４２５６

４０６８２８９－４０６４２５６＝４０３３

と７桁の計算になっちゃいます。

 

でも、先ほどの因数分解を使うと…

２０１７×２０１７－２０１６×２０１６

＝（２０１７＋２０１６）×（２０１７－２０１６）

＝４０３３×１

＝４０３３

と暗算でできちゃうくらい簡単！

 

ＳＡＰＩＸのマンスリーテストの最初の計算でも、この形の計算

は時々出題されています。

 

 

＜因数分解を図形で考えてみる＞

では、どうしてこのように平方数の積は、和と差の積になるのでしょう？

次の計算を図形の面積として考えてみます。

 

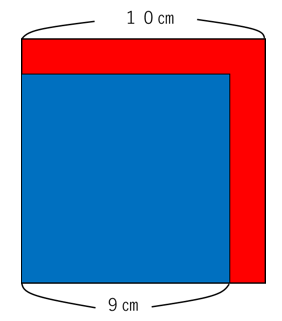
１０×１０－９×９＝

 

１０×１０、というのは１辺10㎝の正方形の面積です。

９×９、というのは１辺９㎝の正方形の面積です。

つまり、１０×１０－９×９というのは、１辺１０㎝の正方形と1辺９㎝の

正方形の面積の差を求める計算ということになります。

 

これを図にしてみます。

 

 

赤色の部分の面積が１０×１０－９×９です。

これを２つの長方形に分けます。

長方形の短いほうの辺の長さは、どちらも１㎝です。

そこで、２つの長方形をくっつけると１つの長方形になり、

縦　１㎝＝１０㎝－９㎝＝１０と９の差

横　１９㎝＝１０㎝＋９㎝＝１０と９の和

となります。

 

つまり、１０×１０－９×９＝（１０＋９）×（１０－９）となるわけです。

 

 

このように、図形の面積をもとにした計算問題というものが

いろいろありますので、みなさんもさがしてみてください。

 

 

因数分解の中にはまだまだ小学生でも使えるものがあります

のでご紹介していこうと思います。お楽しみに！