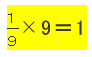みなさん、こんにちは。
受験ドクター算数科の江田です。

気付けば11月。
私が大好きな季節も終わりを迎え、
もうすぐ真冬に突入です(;´･ω･)

特に６年生のお子さんは
入試までの残り２か月、
悔いが残らないよう
全力で頑張りましょう！

ただ、
適度な休憩や睡眠も
しっかり取っていきましょう。

入試直前、はたまた入試当日に
風邪などの体調不良になってしまい、
本番で思うように力を発揮できなかったら、
それこそ悔やんでも悔やみきれないと思いますので。

さて、今日の話題は…
お子さんたちが何気なくやっている
計算についてです。

そう、
タイトルのとおりです。

問題です。

（考え中）
・
・
・

・
・
・
（考え中）
・
・
・
え？
そんなに悩まないって？

あ、失礼いたしました。
答えは…

１？

そうです！
正解です！！

…
……

そんな冷めた表情をなさらないでください…

「この先生は何を言いたいんだ」
という心の声が聞こえてまいります(笑)。

実は、
先日授業を行った生徒と
ある問題について
以下のようなやりとりをしました。

「次のことを頭に入れておこうね。」

「これを頭に入れておけば
0.243243243……
と無限に続く小数も分数に直せるね。」

これは以下のように考えます。

となるわけです。

この問題が理解できて
めでたしめでたし
と思いきや…

そこで生徒がふと疑問を口にしました。

生徒 「あれ？先生おかしくない？」

私 「むっ！？なんと失礼な(￣―￣)
先生はおかしくないぞ！(-“-)
（おかしいところも多々あるけど…）」

生徒 「いや、そうじゃなくて…。
これだと、９倍とか９９倍とか９９９倍とかしても『１』にならないじゃん！」

私 「なぬっ！？するどい質問…」

以上、
実際のやりとり
ほぼそのままです。

みなさん、
おわかりになりましたか。
このお子さんが
一体どこに疑問を持ったのか。

簡単に申し上げますと
今回のタイトルの答えについて…

ということなんです。

なぜなら

となり、
小数点以下に９が無限に続くため、決して『１』にはならない
と考えたのです。

なるほど！
その疑問、納得ですよね。

この疑問に対して、
「近似値」や「有効数字」などの
ことばを使うことができない小学生に対し、
どのような説明をするのがよいのか
少し悩んでしまいました。

悩んだ結果、そのお子さんにした説明は
以下の通りです。

“0.999999……”と“１”との差を考えてみます。

となり、答えは
小数点以下に０が無限に続く
つまり
いつまでも０が続くのだから、この値は０
ということができます。

ということは
「差が０」 すなわち 「同じ値」
ですので、
「0.999999……＝1」
となり、
普段何気なく答えを出している

という計算は正しかった
とわかりました。

いかがでしょう…

今回のように、
おそらくお子さんたちは
普段の学習の中で“ふと疑問に思う”ことが
たくさんあるかと思います。

そんなとき、
“一緒に悩んであげる”ことも
ときには必要なのかも知れませんね。
そうすることによってお子さんは
「あ、僕が疑問に思っていることって、
他の人（大人）でも悩むようなものなんだな」
と感じ、積極的に質問しやすくなると思いますよ^^

もちろん、
“一緒に悩む”だけでいいですよ♪
決して答えを出してあげる必要はありません。

解説は塾の先生に任せればよいのです。

ぜひ、
今後のお子さんとの付き合い方、
声掛けのしかた
の参考にしていただければ幸いです。

それではまた次回♪