皆さま、こんにちは！

前回から、「そもそも偏差値ってなに？」ということを考えています。
今回はその第２回です。
「なんとなく偏差値が大事と思っているけど、実際はよくわかっていないかも…」という方のために解説します。
目標は、偏差値を理解して、必要以上に偏差値に惑わされないようになる、ということです。
偏差値の意味を正しく知って、正しく偏差値と付き合うことを考えましょう。

標準偏差とは何か？

前回は、偏差値の計算方法を簡単に紹介して終わりました。
今回はその続きです。
まず、前回も示した偏差値の計算方法をもう一度見てください。

偏差値を計算するために必要な情報は①自分の点数、②平均点、③標準偏差の３つです。
このうち、自分の点数と平均点はだれでも意味がわかると思いますが、標準偏差とは何でしょう？
実はこの標準偏差という数字が、偏差値という数値を決めるカギになっているのですが、少しわかりにくいです。
今回はこの標準偏差というものについて、理解を深めましょう。

まず、標準偏差の数学的な定義をきちんと書いておきます。
標準偏差とは、データの「分散」という値を計算して、さらにその値の平方根をとった数値です。
ただ、こう言われても数学や統計に詳しい人でなければ、いまひとつピンとこないと思います。
「そもそも分散って何よ？」となりますよね。
「分散」について説明しようとすると、これはこれでそれなりの時間がかかります。
次回以降で「分散」も説明するつもりですが、いまは平均値からのばらつき方を計算していると思ってください。
そして、その平方根（ルート）である標準偏差というものも、同様に平均値からのばらつき方を表します。
では、平均値からのばらつき方とは何でしょうか？

ここでは詳しい統計処理の話はひとまず置いておいて、まずは標準偏差のイメージを理解しましょう。
正しいイメージを理解しておけば、一般的な標準偏差の理解としては十分です。
まずは「標準偏差は平均値からのばらつき具合を表す数字」と覚えましょう。
標準偏差が大きいほど、それぞれのデータの平均値からのばらつきが大きくなります。
おおざっぱに言うと、標準偏差が大きいテストは、受験者の点数の差が大きいということです。
逆に、標準偏差が小さいテストは、受験者の点数の差が小さいということです。
下のグラフのようなイメージを持ってください。

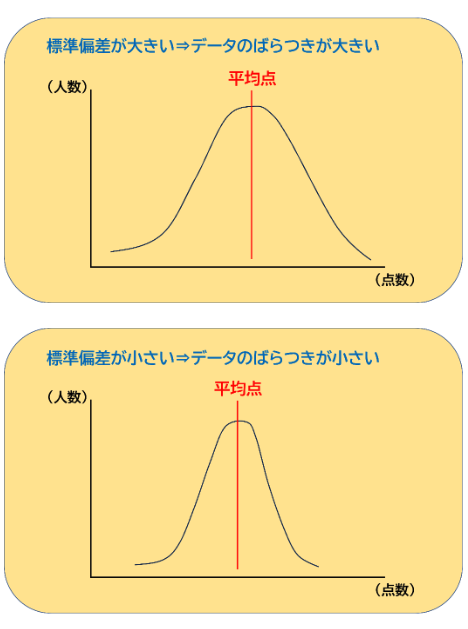
点数と人数でグラフを作ったときに、「山」の裾野が広くなれば標準偏差が大きいということです。
逆に、細長い「山」の形になれば標準偏差が小さいということです。
標準偏差が小さいほど、平均点の近くに多くの人が集中していると考えてもOKです。

テストによって点数の重みが違う

では、この標準偏差が大きい・小さいということが、一体どんな意味を持っているのでしょうか？
それは、それぞれのテストでの点数の「重み」を表現していると理解しましょう。
たとえば、同じ１００点満点をとったとしても、テストによってその意味は少し違います。
ほとんどの人が５０点くらいしかとっていないのに、自分だけ１００点をとったのなら、それはすごいことです。
一方、他にも１００点をとっている人がいるなら、自分の１００点という点数はそこまですごくはありません。
つまり、自分の点数の「重み」は、標準偏差が小さいほど増し、標準偏差が大きいほど減ります。
どういうことかは具体的な数字で考えてみるとわかりやすいです。

たとえば、平均点が５０点で、標準偏差が小さいなら、多くの人は５０点前後の点数をとっているということです。
そのときに、もし自分が１００点をとっているなら、この１００点の「重み」は増すことになります。
なぜなら、１００点をとっている人は少ないはずだからです。
逆に、平均点が５０点で、標準偏差が大きいなら、受験者の点数は５０点から離れたものも多く存在します。
すると、今度は自分が１００点をとっていても、その相対的な「重み」は先ほどの１００点より少し減ります。
なぜなら、今度の場合は１００点を取っている人がそれなりの人数いるはずだからです。

冒頭に紹介した偏差値の計算式では、(自分の点数－平均点)÷標準偏差という計算をしています。
（自分の点数—平均点）の意味は簡単です。
単に、自分の点数が平均点からどれだけ離れているかを求めているだけです。
では、この数字を標準偏差でわるということが何を意味しているかというと、それは「価値」づけしているのです。
わる数が大きくなればなるほど、答えの値は小さくなります。
逆に、わる数が小さくなればなるほど、答えの値は大きくなります。
ですから、自分の点数が平均から１０点離れているとしても、標準偏差が大きいならその値は小さくなります。

小さくしているということは、少し「価値」を下げているということです。
同じ１０点差でも、標準偏差が大きいならその「価値」は低いので、標準偏差でわって値を小さくするのです。
逆もしかりで、標準偏差が小さいならその「価値」は高いので、標準偏差でわって値を大きく修正します。
そうやって「価値」づけされた数字を、さらに１０倍して５０に足したものが偏差値という数字なのです。
ちなみに、最後の１０倍には、深い意味はありません。
そうした方が見た目の数字が大きくなるので、偏差値を見たときにはっきり差がわかりやすいというだけです。

偏差値が示すもの

前回、偏差値は「そのテストでの自分の相対的な位置を知るための数字」と書きました。
しかし、より正確には「そのテストでの自分の点数の価値を表す数字」と表現する方がよいと思います。
簡単に言えば、「そのテストでの自分の点数のすごさ」ということです。

ここで重要なのは、「そのテストでの」という部分です。
先ほどの例でもわかるように、１００点と言っても、すごい１００点とすごくない１００点があるということです。
みんなも同じように１００点をとっているなら、自分の１００点は特にすごいものではないです。
しかし、ほとんどの人が３０点〜４０点しかとれていないのに、自分だけ１００点ならその点数はすごいです。
ですから、偏差値７０と出たら、「今回のテストでのあなたの点数は、とてもすごいです」と言っているのです。
逆に偏差値５０と出たら、「今回のテストでのあなたの点数は、すごくもひどくもないです」と言っているのです。
偏差値という数字が示しているのは、これだけです。
そして、それはあくまでも「今回のテストでの」という条件がついていることに注意してください。
必ずしも次のテストでも同様の偏差値が出るということを意味しているわけではありません。
可能性としてはそうなるはずなのですが、それはあくまで可能性です。

ご存じの方も多いかと思いますが、偏差値という考え方は日本にしかありません。
中学校の理科教員であった桑田昭三先生が独自に研究・考案したものとして知られています。
桑田先生は、テストでの１点の価値を科学的に評価する方法として偏差値の計算方法を考えられたようです。
それが、受験指導において非常にわかりやすく有効であると広く知られ、いまに至っています。
桑田先生によれば、実力が変わっていなくても、偏差値が±３変動する確率は６０％ほどあるそうです。
前回、「偏差値４くらいは誤差の範囲内」と書きましたが、これはあながち間違っていないようです。
桑田先生は他界されていますが、調べてみると偏差値について興味深いことを様々に発言されています。
次回は、考案者の桑田先生が偏差値というものをどう考えていたかについて迫ってみます。

では、また次回お会いしましょう！