皆さま、こんにちは！

前回はつるかめ算の応用として「三段つるかめ」の問題を考えてみました。
ポイントは、「どうしたら自分の知っている形に持ち込めるか？」と考えることでした。
３つある要素を、２つの要素にまとめる工夫をすれば、いつものつるかめ算にすることができました。
今回は、前回とはまた違った工夫の仕方を考えてみましょう。

 

要素をひとつ減らす

問題そのものは前回と同じです。

 

 

前回は、ガムBとガムCの個数比がわかっていることから、ふたつの加重平均を求めてガムBCを作りました。
そうすることで要素をひとつ減らして、いつものつるかめ算に持ち込み、解くことができました。
では、それ以外に解く方法がないのかというと、そんなことはないのです。
要素をひとつ減らすというポイントは一緒なのですが、減らし方に別の工夫の仕方があります。
今回は面積図の下一段をカットする、というテクニックを使ってみましょう。
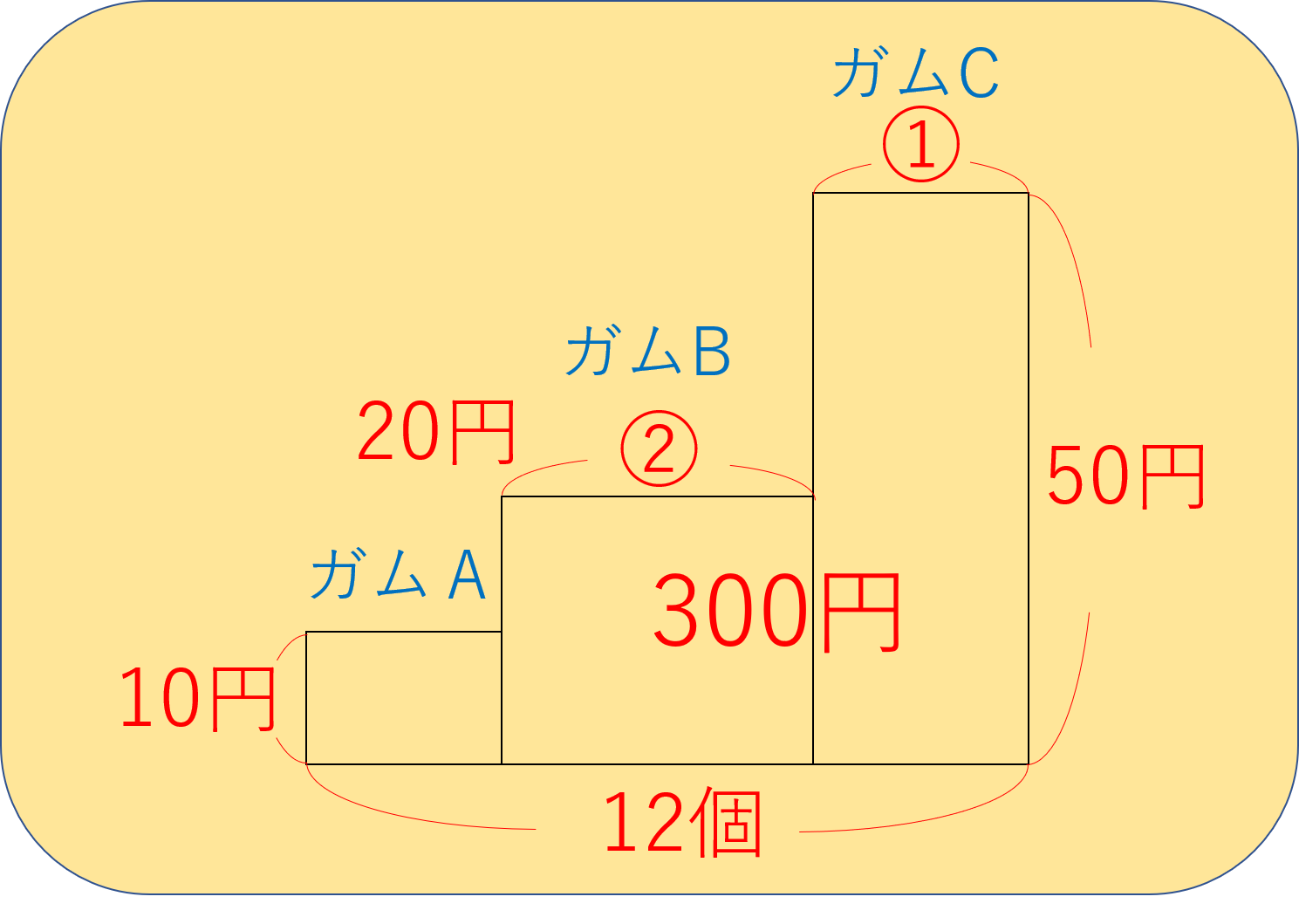
まずは、以下のように三段の面積図を書いてみてください。

 

 

今まで使っていた面積図は左と右の２段のものでした。
しかし、今回は左、真ん中、右の３段になっています。
では、これをどうにかしていつもの２段の面積図にできないでしょうか？
こう考えることが今回の解き方のポイントです。
２段にしたければ、左の１段や、右の１段を取り除くのが一番単純なのですが、それではうまくいきません。
与えられている情報や条件が、うまく活かされないのです。
全体の個数が１２個とわかっていることが重要で、この情報をうまく活かすことを考えます。
すると、下の１段をカットすればいいのではないか、という発想が生まれます。

 

下１段をカットする

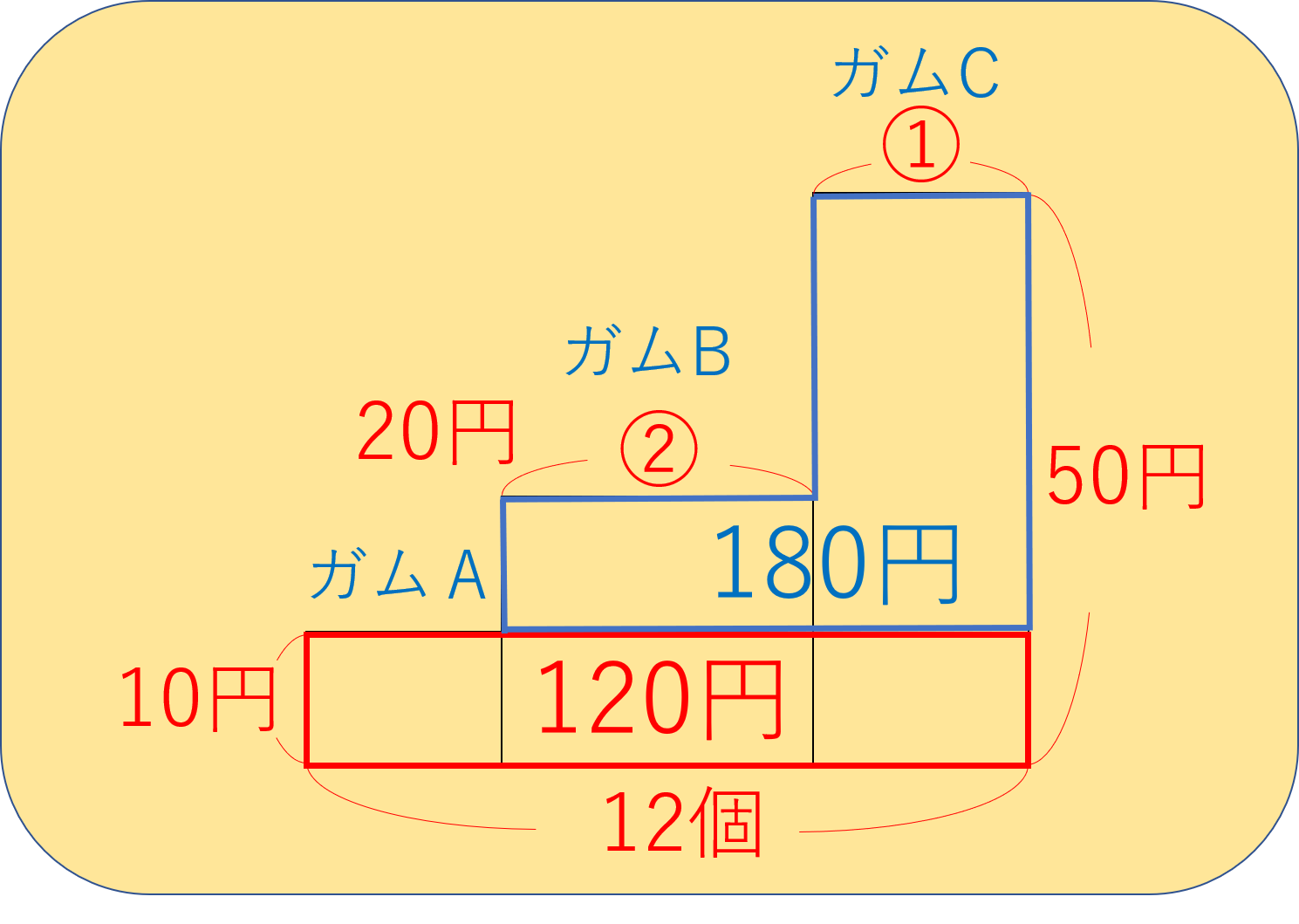
以下のように、１０円の位置で真横に線を入れてみてください。
すると、全体が１２個なので、下１段は１２０円分を表していることになります。
ということは、上の部分は３００円―１２０円で１８０円ということになりますね。
図の中の、赤線で囲まれた部分が１２０円分で、青線で囲まれた部分が１８０円分になるということです。

 

 

さて、このようにふたつの部分に分けてみたときに、上の青線で囲まれた部分の方に注目します。
ここだけ見れば、いつもの２段の面積図です。
これをうまく使えば、この問題を解くことができるのではないでしょうか？
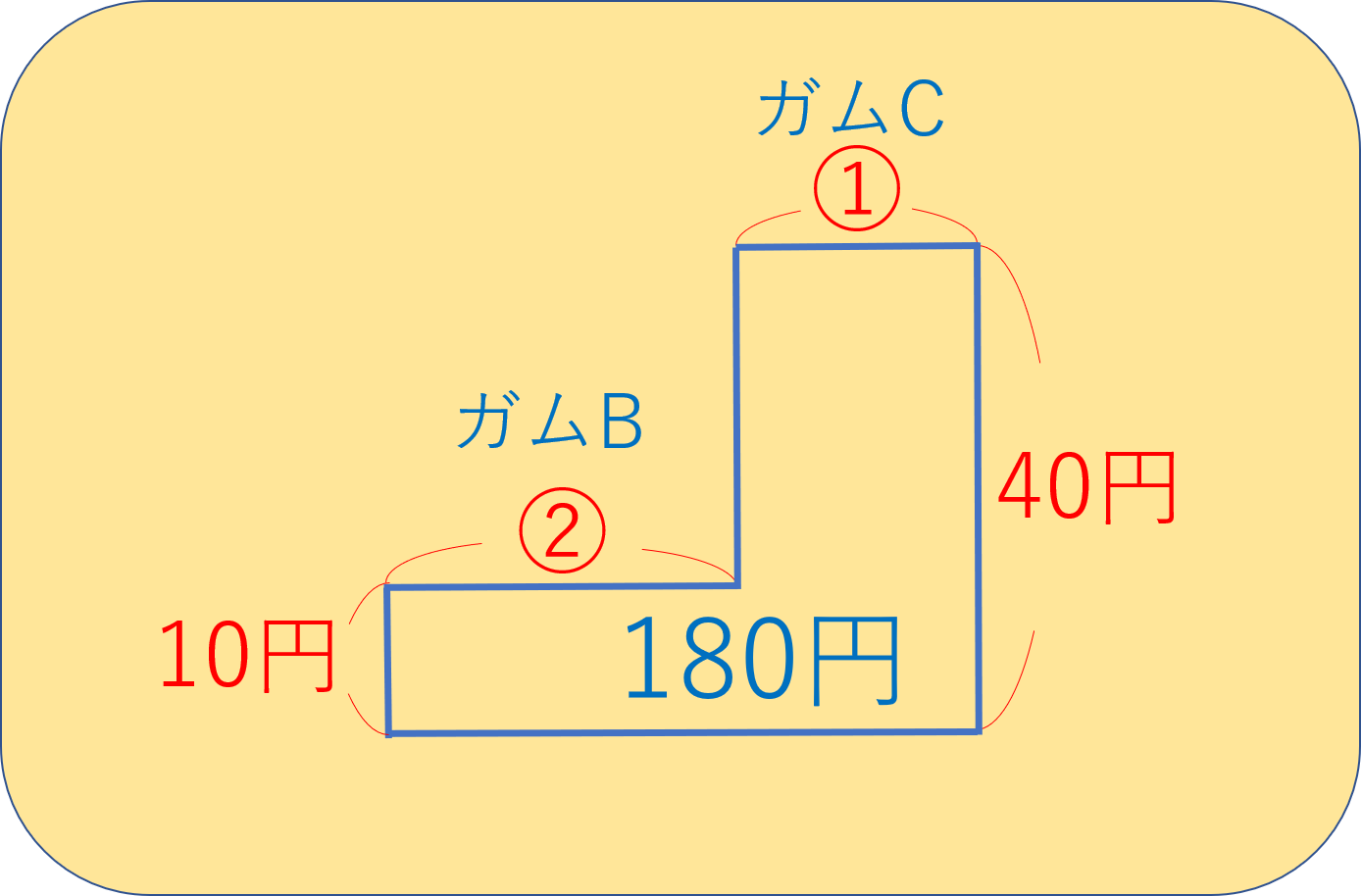
わかりやすくするために、青い部分だけを取り出して図を書き直してみます。
すると、以下のようになります。

 

 

このとき、左のたての長さが１０円、右のたての長さが４０円になっていることに注意してください。
ガムBは２０円、ガムCは５０円ですが、下の１段である１０円分をカットしたので、これでいいのです。
逆に、ここでうっかり左のたてを２０円、右のたてを５０円としてしまうと、正しい答えが出なくなります。
慣れないうちはここでミスが出る可能性があるので、気をつけてください。

 

最後はマルイチ算

ここまでくればあと少しです。
あとはこの面積図を使って、ガムBとガムCの個数を求められればOKです。
ただし、ここでいつもとはちょっと違った処理をする必要が出てきます。
いつもなら、左上の欠けた部分の面積に注目したり、上下２つの面積に分けて考えたりしていました。
しかし、今回はそれではうまくいかないのです。
このような場合は、マルイチ算という処理を使うのが一般的です。
まず、面積図のたてを２つに区切って、ガムBとガムCの２つの長方形に分けてしまいます。
ガムBとガムCの個数比は２：１で、それがそれぞれの横の長さとして②、①と書いてありますね。
これをそのまま具体的な個数、つまり横の長さと考えてしまいます。
たての長さは、左側は１０円、右側は４０円です。
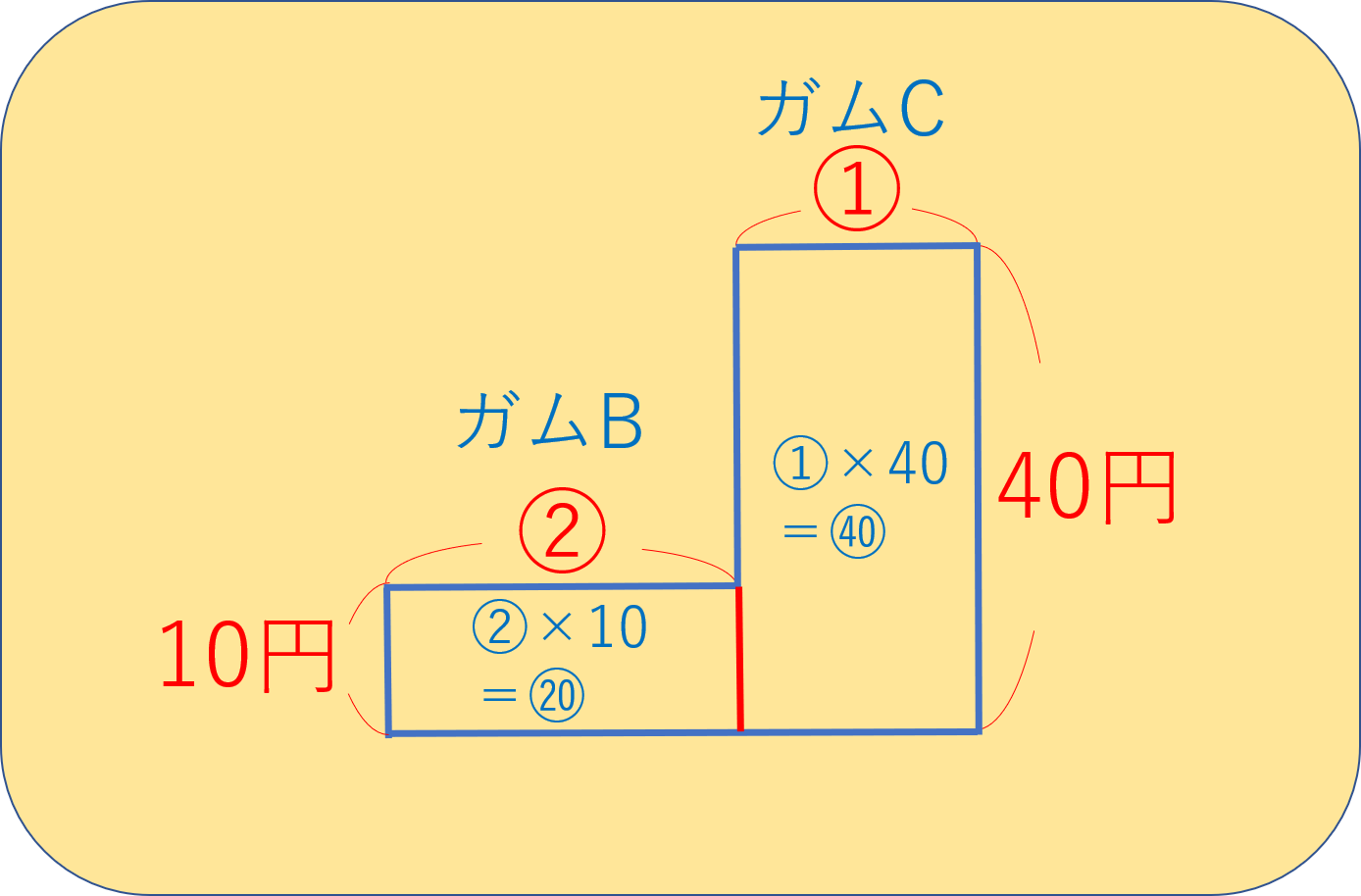
よって、左側のガムBの面積は②×１０＝⑳、右側のガムCの面積は①×４０＝㊵となります。
図に書き込めば以下のようになります。

 

 

すると、合計の面積は60 です。
実際には、この部分の面積は１８０円分でしたよね？
ということは、60 ＝１８０なので、①は１８０÷６０で３を表していることになります。
こうやって①の具体的な値を求めることをマルイチ算と呼びます。
要は、中学生で学習する方程式なのですが、最近の中学受験ではこういった解き方は当たり前に使います。
この機会にぜひ身につけておきましょう。

 

最後はやっぱり確認

さて、①が３と求められましたが、これが何を意味しているかというと、ガムCの個数です。
一方、ガムBの個数は②ですが、これは当然①の２倍で６個ということになります。
ということで、ガムBは６個、ガムCは３個ということになりますが、ではガムAは何個でしょう？
ガムの個数は全部で１２個でしたから、１２－（６＋３）＝３で、３個となりますね。
求めるものは、ガムAの個数でしたから、これで答えは３個ということになります。
ただしここであせらずに、この個数が問題文の条件を満たしているか、最後に確認してみましょう。
前回も書いたように、大切なことは確認することです。
ガムAは１０円で３個、ガムBは２０円で６個、ガムCは５０円で３個です。
よって、１０×３＋２０×６＋５０×３＝３０＋１２０＋１５０＝３００となりますから、合計金額は３００円です。
ちゃんと問題文の条件を満たしていますね！
ということで、今回も無事に答えにたどり着くことができました。

 

今回のまとめ

いかがでしたでしょうか？
前回とはまた違った方法でしたが、今回も「三段つるかめ」の問題をちゃんと解くことができました。
上級者を目指すのであれば、１通りの解法で満足せずに、「他に解き方はないのかな？」と考えてください。
ひとつの問題に対していくつ解法が思い浮かぶかで、算数の底力や応用力がわかります。
複数の解法が思い浮かぶ方が、問題を解く幅が広がるので、様々な状況に対応できる可能性が上がります。
逆に、「このやり方しかできない」という状態だと、そのやり方が使いにくい状況になったときに困りますね。
実際に、前回解説した加重平均を使う解法は、問題によっては途中で数値が分数になることがあります。
分数になっても気にせずに計算すれば答えはちゃんと出るのですが、あまり分数計算はしたくないですよね。
しかも、金額が途中で分数になってしまうと、最終的には答えが整数になるとしても、ちょっと違和感があります。
そういったときに、今回のような解法も知っていれば、分数の処理を避けるということもできるのです。
解法をたくさん知っていて損をすることは絶対にありません。
ぜひ様々な解法にトライしてみてください。

では、また次回お会いしましょう！