皆さま、こんにちは！

前回からつるかめ算についてのお話をしています。
今回はその第２弾です。
前回は、つるかめ算ってそもそもどういう問題なのか？
どういうときにつるかめ算を使えばいいのか？
そんなことについて解説しました。
結論としては、「２種類の合計が出てきている」なら、つるかめ算だ、ということでしたね。
問題を見たときに、「あ、これはつるかめ算だな！」と、ピンとくるように意識して練習しましょうとお伝えしました。

では、今回はつるかめ算の処理の仕方について考えてみましょう。
前回、つるかめ算の処理の仕方は色々あると書きました。
まず、もっとも原始的でだれでも解ける方法から考えてみましょう。
それは、表を作って書き出すという方法です。
地道に全パターンを調べるのです。
ためしに、前回に例で挙げた問題を、表を作って解いてみましょう。

この問題であれば、たとえば次のような表を作ります。

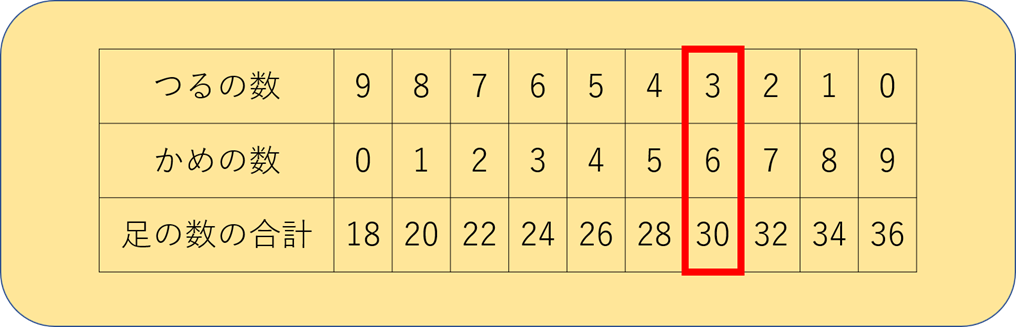
つるの数が９羽、かめの数が0匹からはじめて、順番に数を変化させていきます。
すると、つるが３羽、かめが６匹のときに、足の数の合計が３０本になるのがわかります。
すべて書き出したので、一目瞭然ですね！
それはそうだけど…、でも、こんなことを毎回やるのは面倒くさい…。
もちろん、そうですね。
しかし、こういった地道な作業を面倒くさがったり、バカにしたりしてはダメです。

中学入試の算数の問題では、「調べ上げ」といって地道に書き出して調べる必要がある問題が存在します。
生徒には「面倒くさがり屋かどうかの判定問題だよ」と私は言ったりします。
正しく書き出せる、表を作れる、というのは、算数の大切なテクニックのひとつなのです。
こういった作業は、簡単なようでも慣れていないとスムーズにできないものです。
意識して練習しておかないと、いざ必要になったときに困ります。
フリーハンドできれいな表を作るというのは、やってみればわかりますが、案外難しいのです。
さらに、どんな問題でも地道に調べれば何とかなる！と理解している方が、実戦でも強いです。
ですから、こんな簡単なつるかめ算でも、まずは調べてみるということを最初に経験しておくべきです。

また、先ほどの表を作ってみると、よりスマートな解法の理屈もきちんと理解できます。
まずは片一方だけにしてみて、そこから変化を考えるという処理の仕方です。
足の数の合計の変化に注目してみましょう。

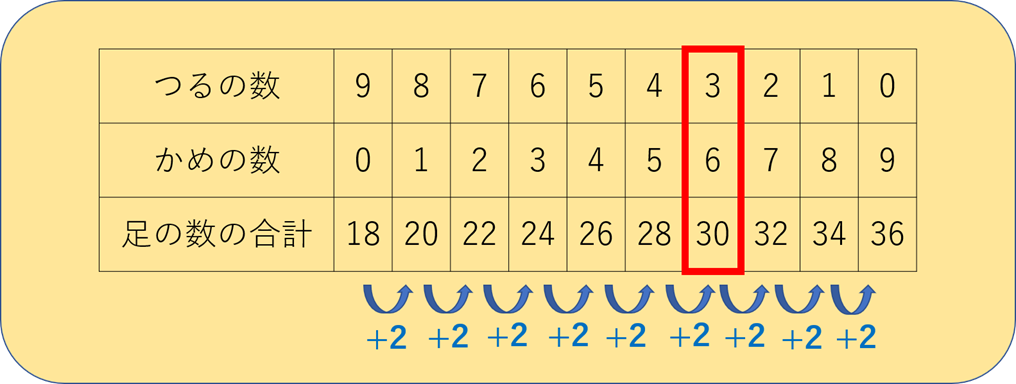
足の数の合計は２本ずつ増えてますね？
つるの足は２本、かめの足は４本なので、つるとかめをひとつ入れ替えると、足の数の合計は２本増えます。
つるが９羽でかめが０匹のときは足の数の合計は１８本なので、３０本にするには１２本増やす必要があります。
１２÷２＝６なので、つるとかめを６つ入れ替えればよいということになります。
よって、つるが３羽でかめが６匹、が答えです。
これは、とても重要な解法で、特に面積図が使いづらい弁償算というタイプの問題で役に立ちます。
これをひとつの公式として暗記的に覚えているお子さんもいますが、ただの丸暗記では危険です。
正しいイメージを伴って覚えていないと、応用も利かないですし、解き方を忘れてしまうとアウトです。
まずは片一方だけにしてみて、そこから変化を考えるというのは、算数においてとても重要な感覚です。
また、表に整理してみて、何かそこに法則性がないか考えるというのも、同様に重要な感覚です。
こういったことを身につける入り口としてつるかめ算をとらえた方が、より深い学びにつながります。

忘れてしまうと言えば、「解き方をすぐに忘れてしまうよー」、というお悩みをお持ちの人は多いと思います。
忘れてしまう理由は色々と考えられます。
ひとつの原因としては、最初に面倒くさい解き方を経験していない、ということがあると思います。
最初に便利な解き方を教えてもらうと、それはただ「やり方」として与えられたものにしかならないです。
簡単に与えられたものだから、すぐに忘れてしまうのです。
「Easy come, easy go」ということわざが英語にありますが、まさにそれです。
しかし、面倒くさいやり方をたくさん経験したあとで、便利な解き方を教えてもらうと、その意味が変わってきます。
「すごい！」とか「なんて便利なんだ！」とか、そこに感動があるかどうかが重要なのです。
「これを覚えておけば、あんな面倒くさい作業をしなくていいんだ！」と思えば、忘れないようにするでしょう？
ですから、最初はたくさん面倒くさい思いをした方がいいのです。
こういった意味でも、つるかめ算をまずは地道に調べて解く、ということを経験させるのは良いことです。

ということで今回はここまでです。
その問題を通して、何を学び、どういったことを身につけるのか？
ただ問題が解ければ良いのではなくて、学んでいる内容を意識してトレーニングしてみてください。
そして、ちょっと遠回りでも少し面倒くさい作業を経ることで、正しく理解し忘れないということを目指してください。
急がば回れ、です。
では、また次回お会いしましょう！