皆さま、こんにちは！
さて、前回は少し寄り道をして、「平均」そのものについて、少し考えてみました。
今回は、話を本題に戻して、前々回まで扱っていた「加重平均」というタイプの問題の続きです。
まずは下の問題を考えてみてください。

速さについての問題ですが、速さの学習を始めたばかりのお子様だと、わりと間違えの多いものです。
一番多い間違いは、行きと帰りの速さの平均を単純にとってしまうことです。
２つの平均だから、（５＋15）÷２＝10で、毎時10㎞だな、とやってはダメなのです。
なぜでしょうか？

ポイントは「往復の平均の速さ」という質問の仕方です。
この言葉にだまされてはいけません。
速さは、道のり÷時間で求められますね？
道のりを時間で割ることで求められる速さというのは、そもそもすべてが「平均の速さ」なのです。

毎時5㎞で行くと言っても、最初から最後までずっと毎時5㎞ということはないですよね？
スタートするときは、だんだんと速くなるわけですし、止まるときも徐々に減速して止まります。
実際には、毎時5㎞よりも遅いときもあれば、速くなっている瞬間もあるわけです。
ですから、道のり÷時間という計算で求めているのは、平均すればこのくらいの速さ、ということなのです。
これは0.1秒とか、0.0001秒とか、どんなに短い時間の場合でも、「平均の速さ」であることは変わりません。

中学や高校の物理で学習することですが、そもそも速さには「平均の速さ」と「瞬間の速さ」があります。
「瞬間の速さ」を求めることは、算数では基本的にはできません。
「瞬間の速さ」を求めるためには、高校で学習する微分という数学の知識が必要だからです。
ですから、算数で考えている速さというのは、基本的にすべて「平均の速さ」だと理解しておきましょう。

こう理解できるようになると、速さ同士を足して２で割るようなことはできないということがわかります。
前々回のブログで、「平均を足して２で割ってはいけない」という話が出てきたことを思い出してください。
例えば、男子１０人の平均が６０点で、女子２０人の平均が６６点のテストがあるとします。
このとき、全員の平均点は（60＋66）÷２＝63で、63点とはできません。
正しくは、全員の合計点を全員の人数で割ることで求められます。
ですから、（60×10＋66×20）÷（10＋20）＝64で、平均点は64点とするのが正しいです。
これと同じことが、今回の速さの問題でも成り立っているのです。

そもそも算数であつかう速さというのは、すべて「平均の速さ」でしたね？
ですから、「往復の平均の速さ」というのは、何のことはない、単に「往復の速さ」と考えていいのです。
そして、行きと帰りの速さを、そのまま足して2で割ることもできません。
じゃあどうすればいいかというと、単純に「往復の道のり÷往復の時間」とすればいいのです。
ちょっと計算してみましょう。

まず、往復の道のりは、片道の２倍で良いですから、10㎞×２で２０㎞ですね。
次に、往復にかかる時間を求めてみましょう。
行きは、毎時5㎞なので、10÷５＝２で、２時間かかります。
帰りは、毎時１５㎞なので、１０÷１５＝2/3で2/3時間（40分）です。
よって往復では、２時間＋2/3時間で、8/3時間かかります。
ですので、往復の速さは２０÷8/3＝7.5で、毎時7.5㎞が正解になります。

さて、以上でこの問題の解説自体は終わりなのですが、ここでもう一歩踏み込んで考えてみましょう。
冒頭で（５＋15）÷２＝10で、毎時10㎞とするのは間違いだと解説しました。
この10という値は、５と１５という値の単純な真ん中です。
毎時7.5㎞というのが正しい答えですが、この7.5という値は、真ん中の10よりも５の方に近いです。
これって、なにかと似ていないでしょうか？
そうです、前々回に解説した全体の平均は「重い」値の方に「引っ張られる」という、あれです。
こんな図が出てきたのを思い出してください。

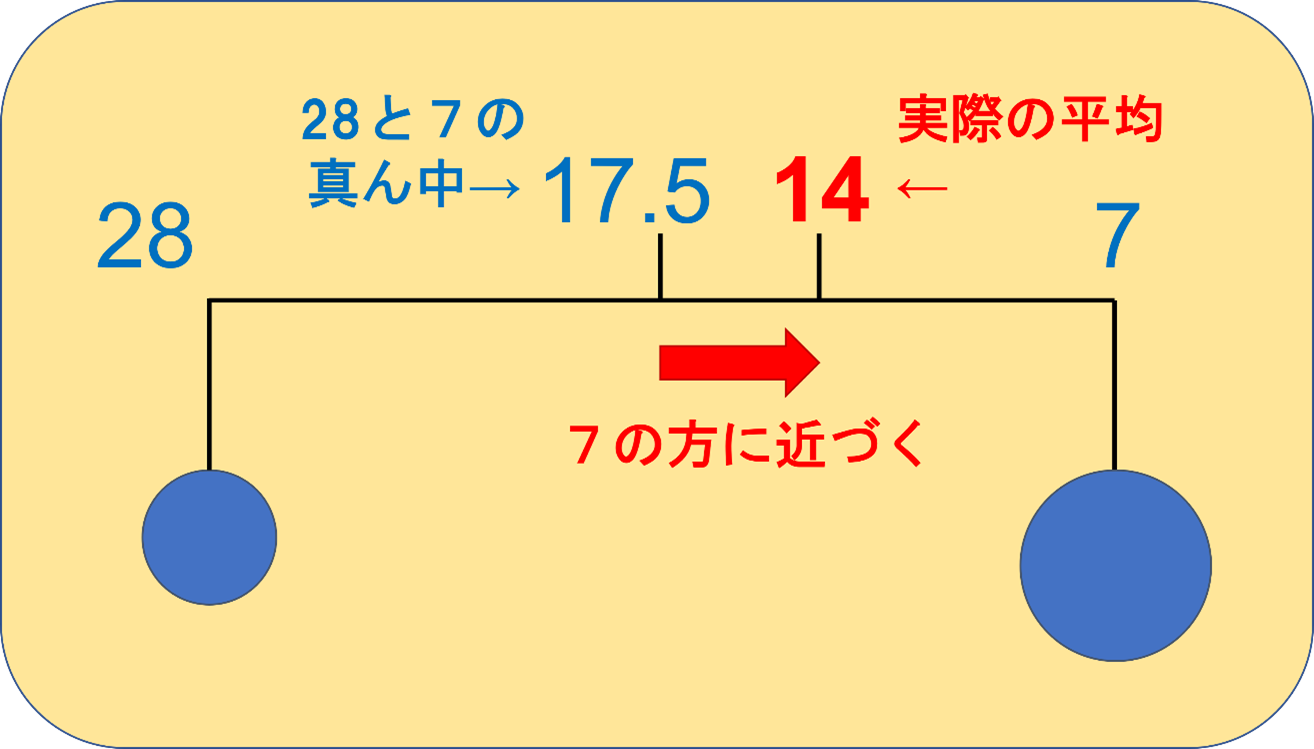
実は今回の速さの問題も、これとまったく同じ理屈が成立します。

つまり、今回の問題も「加重平均」の一種と考えることができるのです。
そもそも、行きの毎時5㎞と、帰りの毎時15㎞で、どちらの方が長い時間その速さで動いていますか？
先ほども計算したように、毎時5㎞の方は2時間で、毎時15㎞の方は2/3時間です。
ですから、毎時5㎞で動いている時間の方が長いわけです。
ということは、往復の平均の速さを考えると、より長い時間動いている毎時5㎞の方に引っ張られるのです。
毎時5㎞の方が値として「重い」ということです。

ここまでが理解できると、じゃあこの問題もてんびん算で解けるのかな？となります。
はい、解けます。
ただし、これは一般的な解法ではないですし、私自身も普段からこのような解き方はしていないです。
あくまで、同様の理屈が成り立っていることの一例として、あえててんびん算でやってみたいと思います。

まず、往復の平均の速さをてんびん算で処理するには、てんびんに引っ掛けるおもりは「時間」にします。
「時間」は具体的に120分と40分としても良いですし、比を使って３：１としても良いです。
しかし、具体的な時間を求めるなら、「往復の距離÷往復の時間」とやってしまう方が早いですね。
ですので、ここはあえて比にしましょう。
片道の距離は一緒ですから、速さ比が5：15＝１：３なら、時間比は逆比で３：１です。
こうできるなら、具体的な時間は求めなくても良いです。
速さはおもりの上に書いておきます。
すると、このような図ができますね。

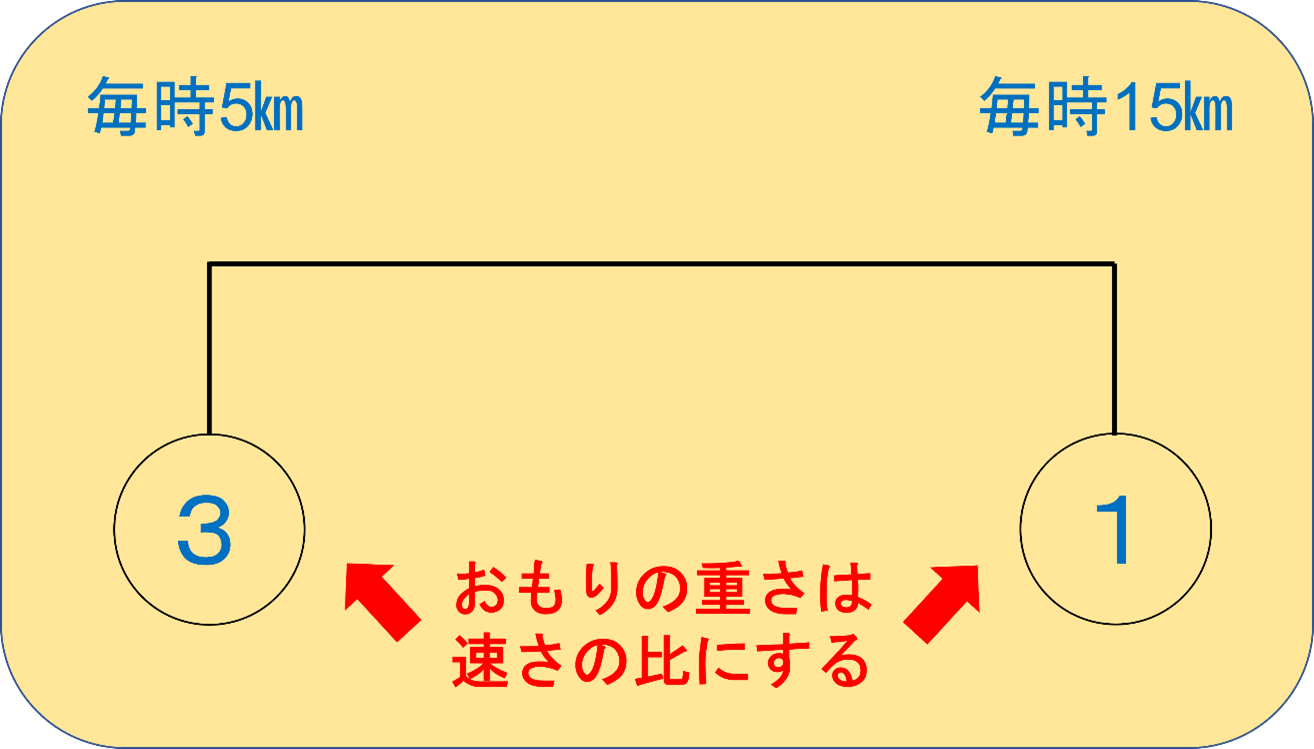
つりあいのとれるポイントは、重さの逆比で１：３のところです。
また、毎時5㎞と毎時15㎞の差は、毎時10㎞です。
これらを図に書き加えると、こうなります。

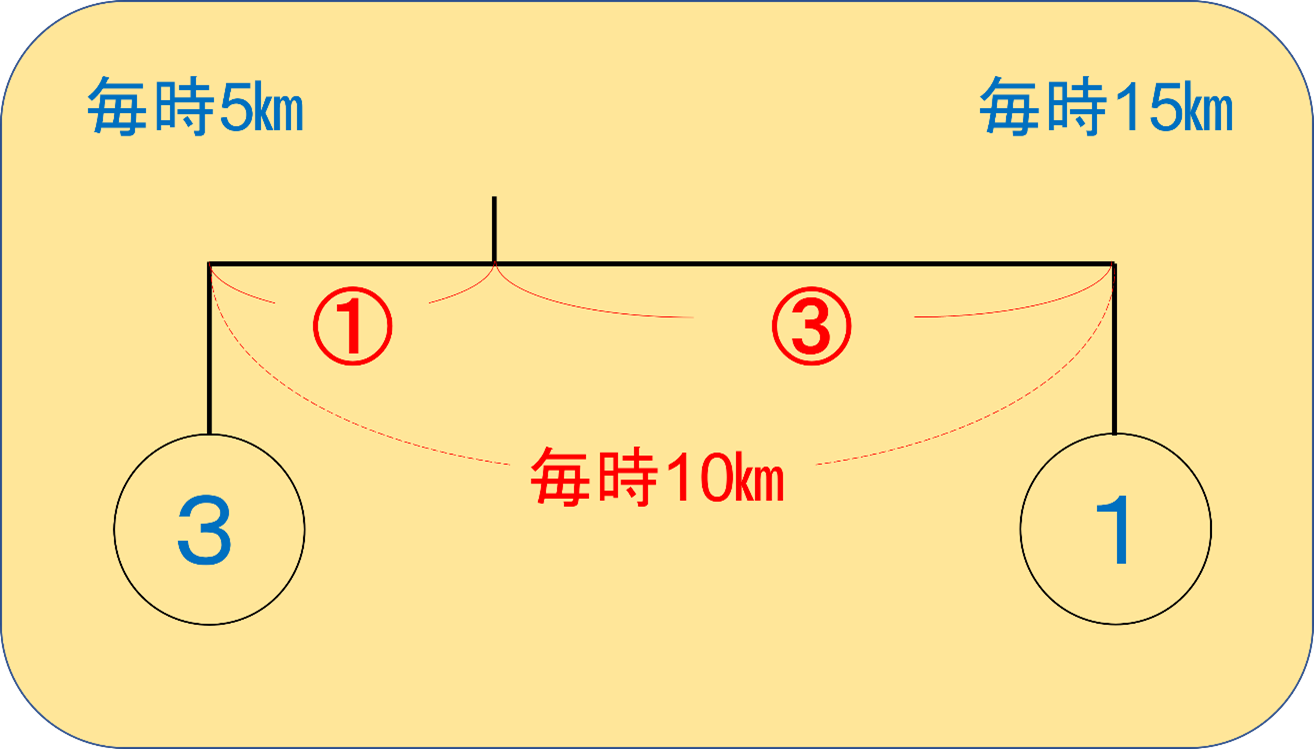
あとは、ふたつの差である毎時10㎞を１：３で比例配分すれば良いですね。
すると、こんな感じになります。

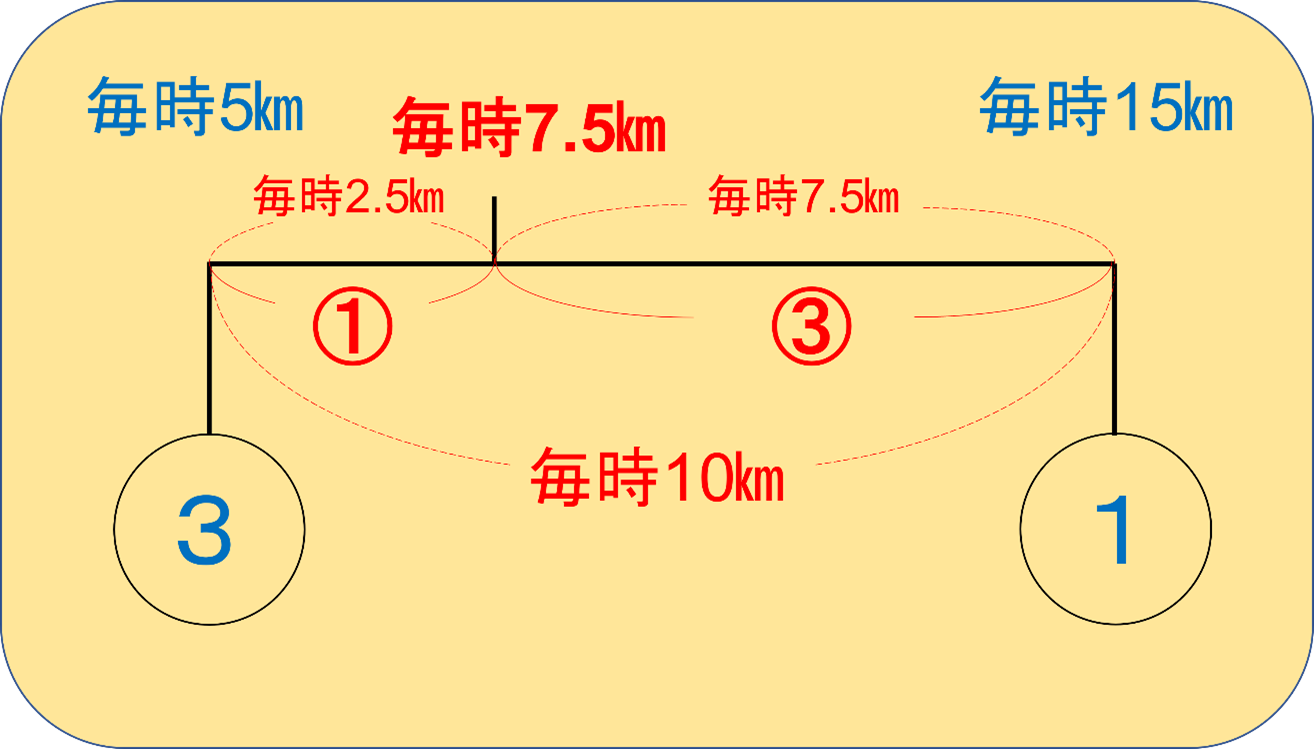
すると、どうでしょう？
ちゃんと、毎時7.5㎞という答えにたどり着きましたね！
ということで、今回の問題も、「加重平均」の一種ということで、ちゃんとてんびん算で処理できるのでした。

いかがでしたか？
最初に扱った食塩水の混ぜ合わせも、前回扱った平均の問題も、すべててんびん算で処理できました。
そして、今回の速さの問題もやはりてんびん算で処理できました。
ぱっと見は違って見えても、本質的には同じ問題だということが、今回もわかっていただけましたでしょうか？
次回は、このテーマの最後として、図形の問題でも同じ理屈が成り立つ例を紹介します。
お楽しみに。

では、また次回お会いしましょう！