皆さま、こんにちは！
さて、前回は算数の食塩水の問題について、てんびん算という考え方を紹介しました。
まずは前回のおさらいを少ししておきましょう。
以下のような問題をどう考えるかということでした。

基本となるのは、濃度、食塩水の量、食塩の量をビーカー図に整理していくことです。

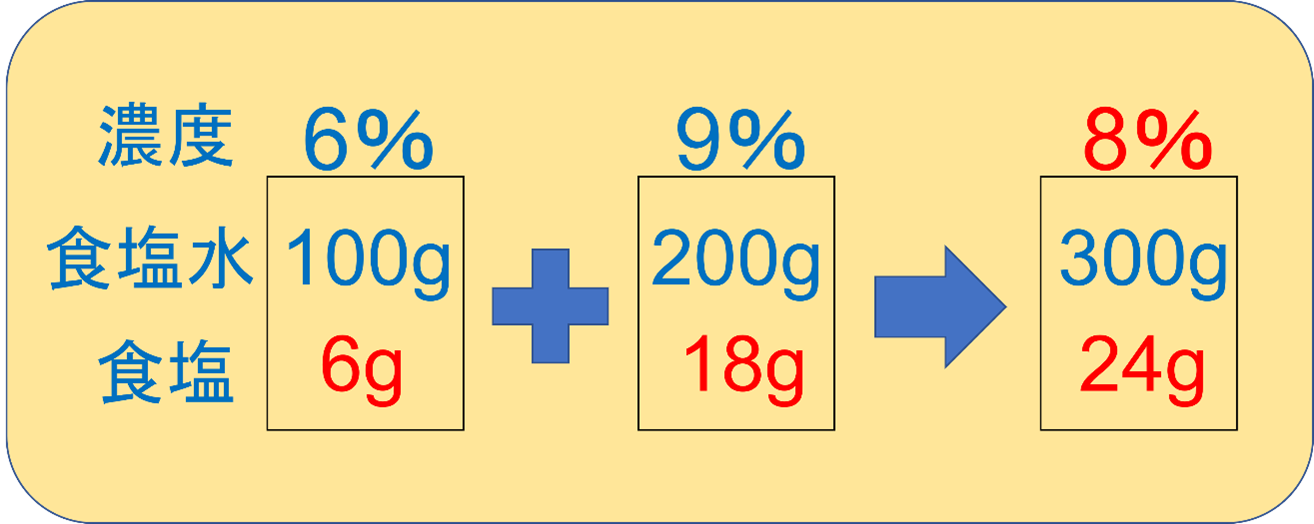
ビーカー図の書き方は人によって少し違いますが、3つの要素をすべて整理していくという点は一緒です。
このように書き出して整理していけば、答えは８％とわかります。
これができるのは前提として、さらにてんびん算という考え方を身につけると、解くのが速く楽になります。
詳しい解説は前回のブログをお読みいただくとして、結論としては以下のような図を書きます。



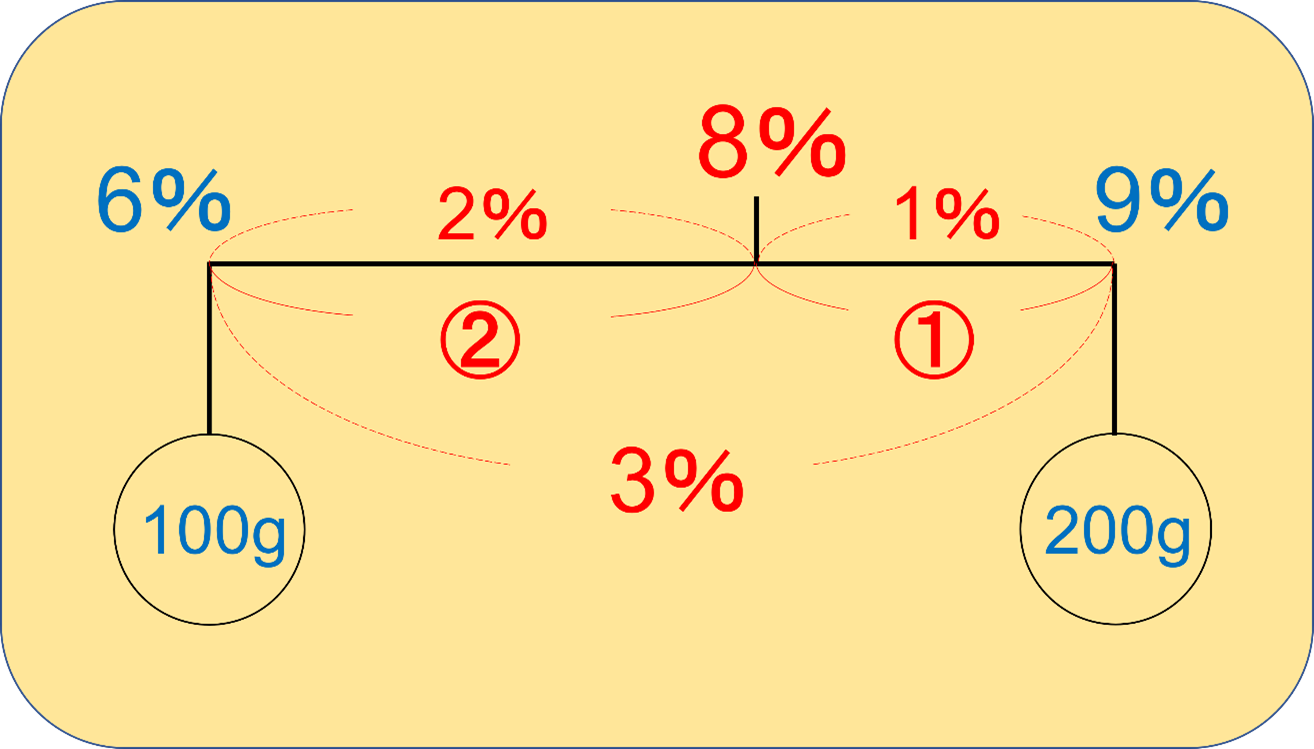
この解法の利点は、食塩の量を一切求めなくても答えが出せるということです。
慣れてくれば、作業としてはビーカー図を書くよりは圧倒的に楽です。
計算ミスをする可能性もこちらの方が少ないと思います。

今回のテーマは、この考え方を他の食塩水の問題にも応用してみよう、ということです。
食塩水同士の混ぜ合わせだけではなく、水を加えたり、食塩を加えたりする場合も、同様に処理できます。
ためしにやってみましょう！

まずは、水を加えてうすめる場合を考えてみます。
以下のような問題を考えてみてください。

まずは基本通りにビーカー図に整理してみます。
水なので、溶けている食塩の量はもちろん０gです。
すると以下のように整理することができます。

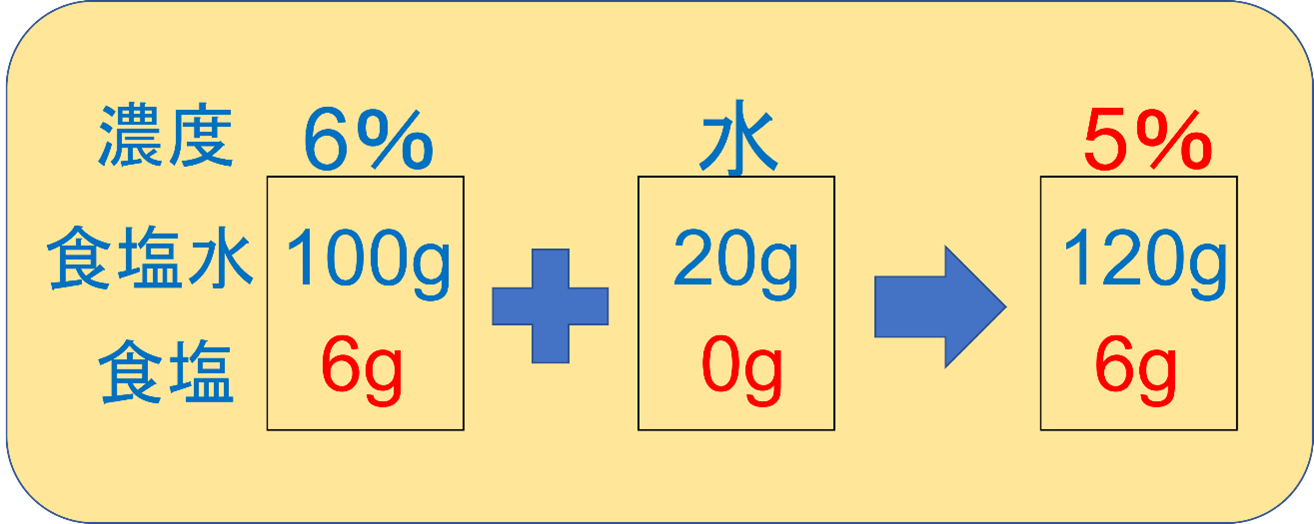
混ぜた後の食塩水の量は120gで、解けている食塩の量は20gです。
よって、６÷120×100＝５となりますから、答えは５％です。

ではこれを、てんびん算で処理するにはどうしたらいいでしょうか？
この場合は、水の方の濃度をどうするかがポイントなのですが、それは当たり前に考えればよいです。
食塩がまったく溶けていないのですから、濃度は0％でOKです。
すると次のようなてんびん図が書けます。

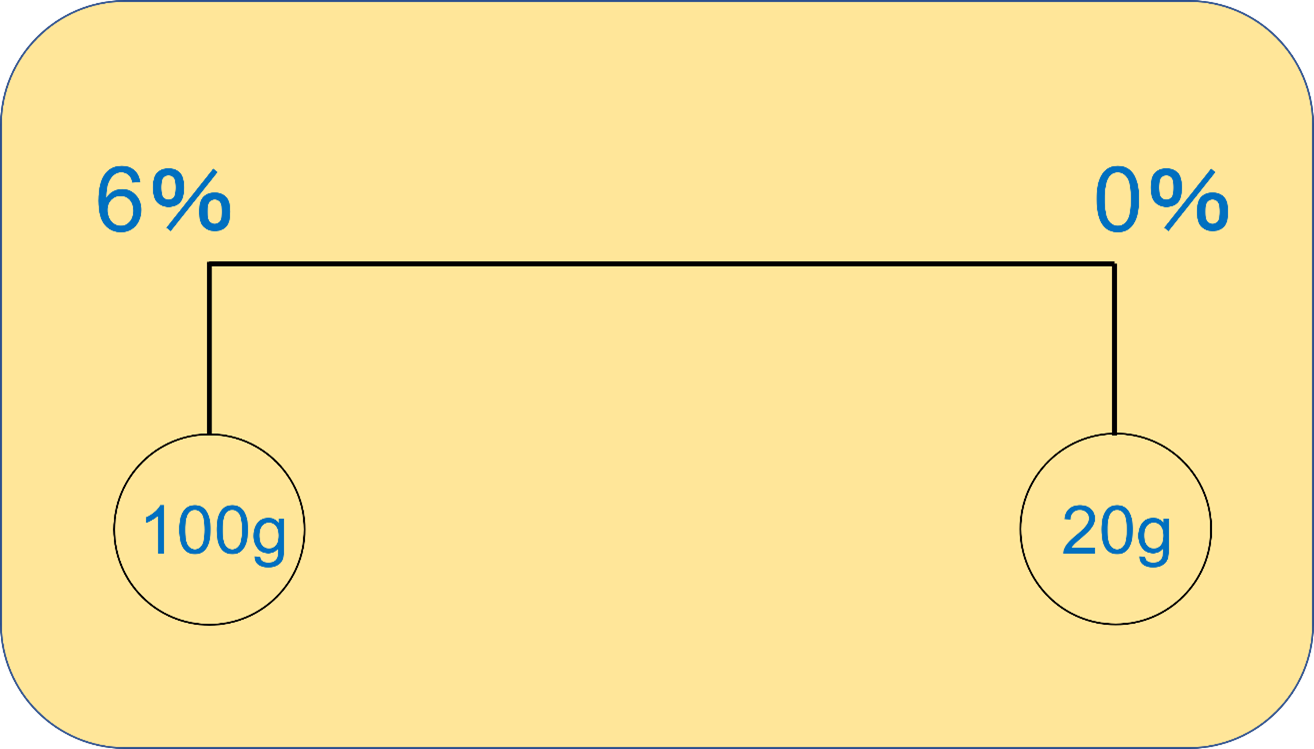
右側に書いてあるのが水の状態です。
100：20＝５：１なので、つりあいがとれる場所は左端から見て１：５のところになります。
すると以下のような図が完成して答えは５％となります。

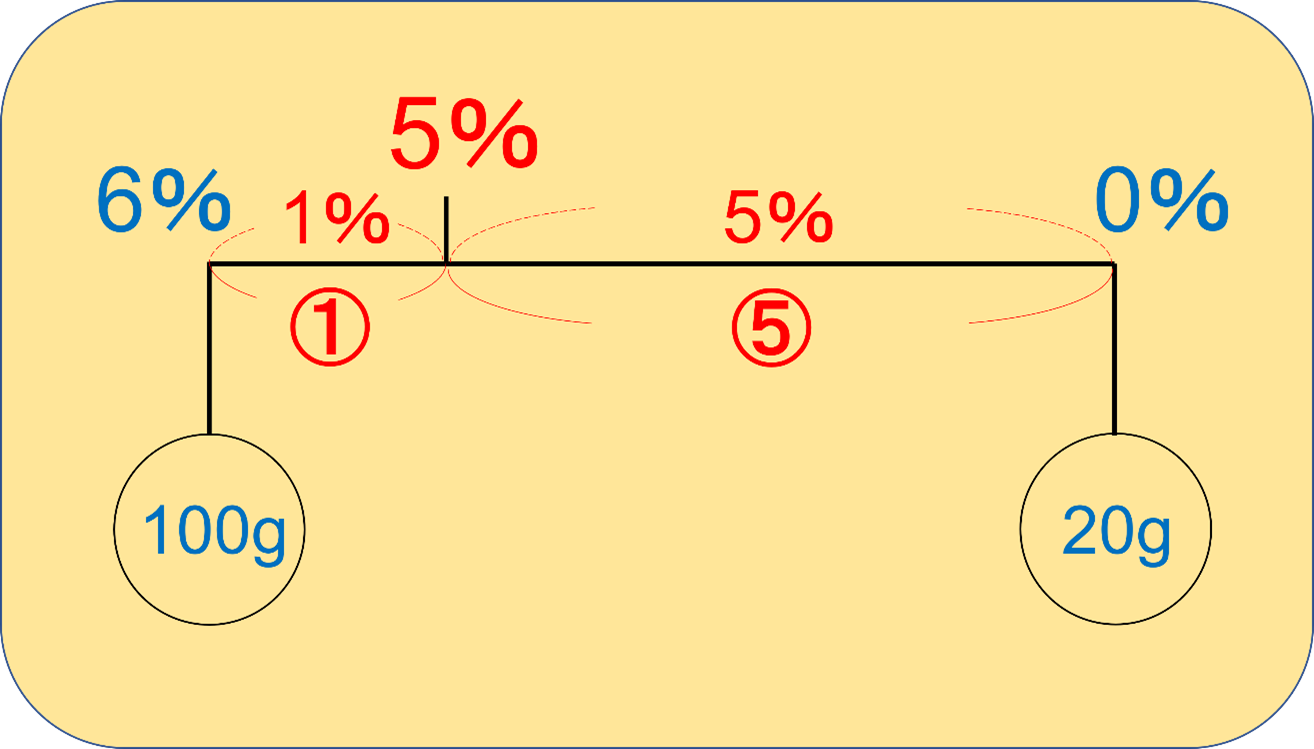
ビーカー図を書いて考えた答えと、ちゃんと同じになりましたね！

では、次のような問題はどうでしょうか？

今度は食塩を加えて濃くしようということですね。
これもビーカー図に整理して考えてみると、以下のようになります。



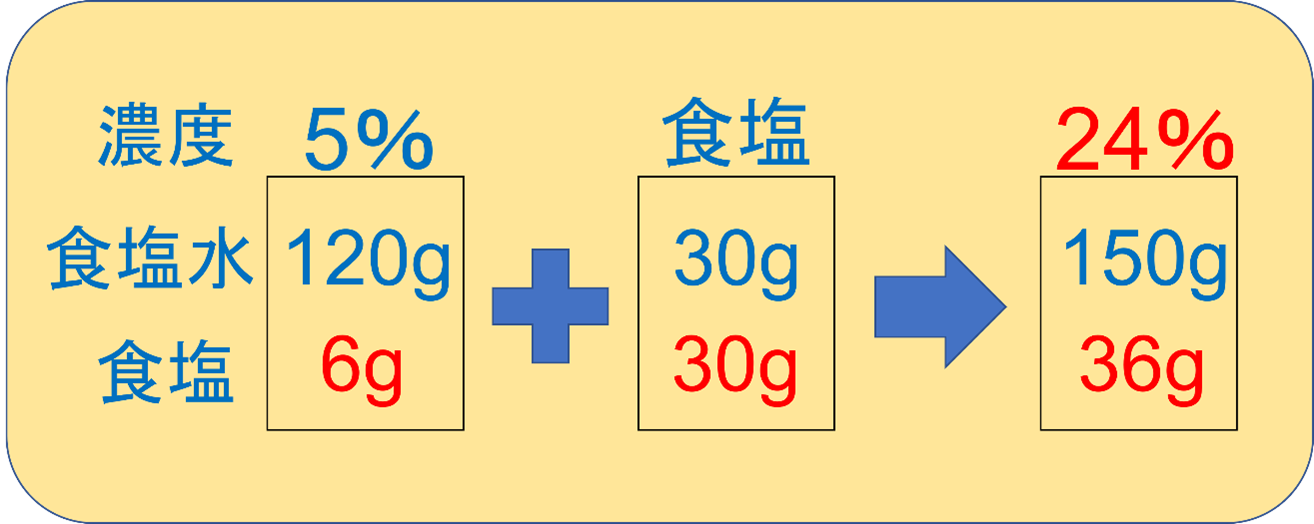
このような場合は、食塩を加えたときに、食塩水の量も同じだけ増えていることに注意してください。
すると、できあがる食塩水は150gで、溶けている食塩の量は36ｇになります。
よって、36÷150×100＝24で、答えは24％になりますね。

ではこれを、てんびん算でも処理してみましょう。
この場合も、食塩の方の濃度をどうするかがポイントなのですが、これも当たり前に考えればＯＫです。
食塩だけなのですから、濃度は100％です。
すると次のようなてんびん図が書けます。

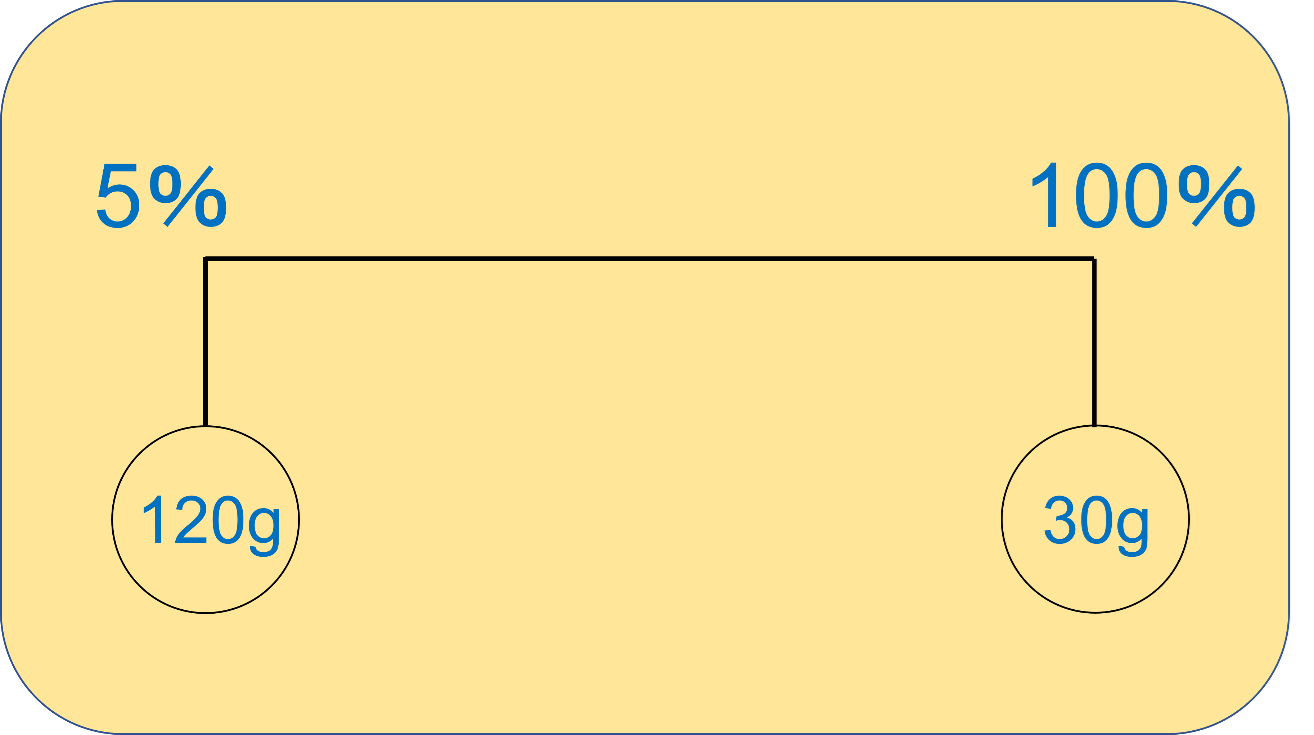
右側に書いてあるのが食塩の状態です。
120：30＝４：１なので、左端から見て１：４の場所でつりあうことになります。
すると、以下のような図が完成します。
このときに、２つの濃度の差を、比例配分しないといけないことに気をつけてください。
つまり、左右の濃度の差は９５％なので、これを１：４に分けると、１９％と７６％になるということです。
５％＋１９％＝２４％になり、100％－７６％＝２４％になるので、つじつまはあっていますね。



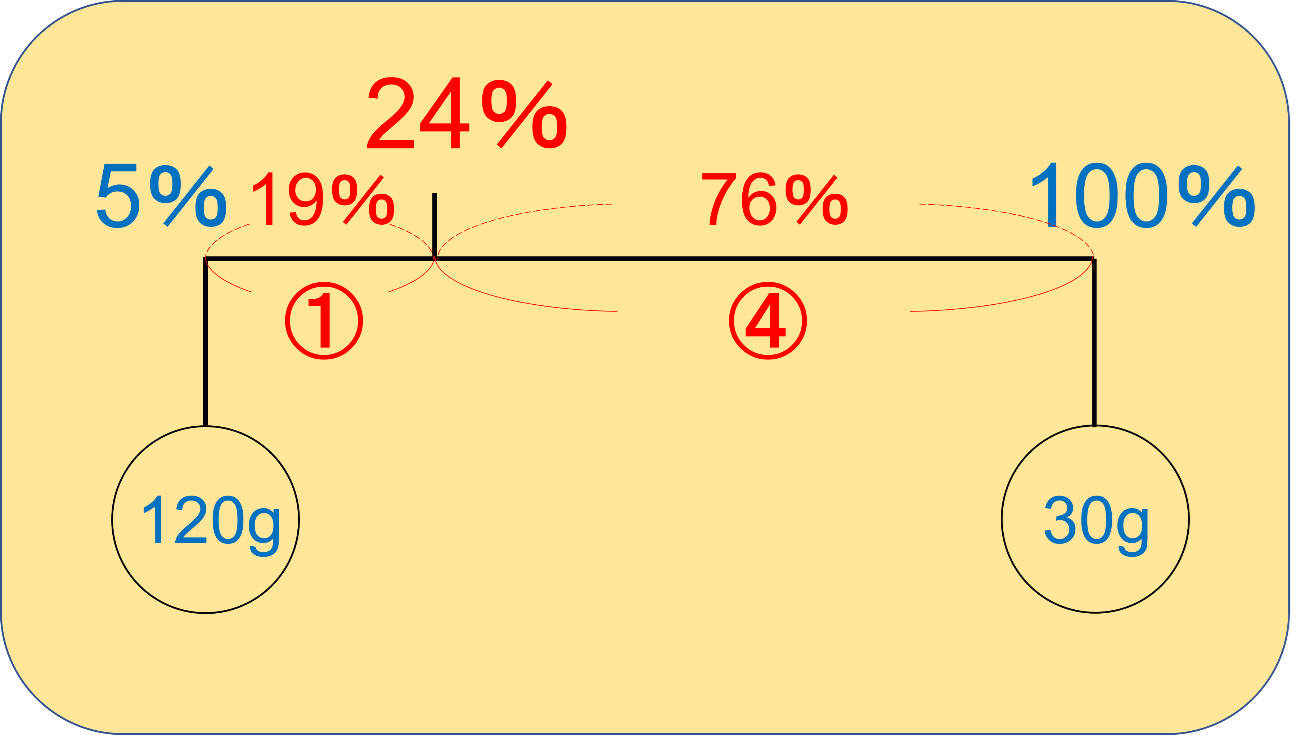
ということで、この場合も無事に２４％という答えにたどり着きました。
やはりてんびん算が使えるということがわかりましたね！

いかがでしたでしょうか？
このように、上手く使えばてんびん算は様々な混ぜ合わせの問題に利用できます。
今回は解説できませんでしたが、水を蒸発させる問題などもてんびん算を書く手順を工夫すれば解けます。
そして、食塩水の問題でなくても、同じような原理が背後にある問題なら、同様の処理が可能です。
次回は、平均の問題に対して、てんびん算がどのように利用できるかを考えてみます。
お楽しみに！

では、また次回お会いしましょう！