皆さま、こんにちは！
３月になりました。
受験シーズンも完全に過ぎ去り、本格的に新年度の雰囲気になってきていますね。
新学年の勉強も、もうすぐ1か月分が終わるころです。
ここまでの振り返りをしっかりして、良いスタートが切れたね！となるようにしていきましょう。

ということで、今日は、いまのうちにこれだけは確認しておきたい！ということをテーマにしました。
テーマは「平面図形と比」です。
まだ習ってないよ、というお子さんでも大丈夫！
今日のブログで扱う内容は、学年は関係ないようにしてあります。
教わったことがなくても、この場でわかる内容に限定してあります。
逆に言えば、すでに学習済みのお子さんには、これはもちろんわかっているよね？という内容です。
ぜひお家で確認してみてください。

「平面図形と比」は、数学では「相似」ともいいますね（大人向けの文章なので、以下は「相似」と書きます）。
中学入試においても、「相似」は最重要テーマのひとつです。
平面図形でも立体でも、問題の中で「相似」を頻繁に利用することになります。
また、理科でも、例えば「凸レンズ」や「地層の傾き」などを考えるときに、やはり「相似」の感覚は重要です。
「相似」を制す者は中学入試を制す！
ここまで言うと、ちょっと言いすぎかもしれませんが、でもそのくらい重要な単元です。

さて、では「相似」において、いったい何がきちんとできていないとダメでしょうか？
それは、適切に相似形を見つける！ということです。
これが応用問題への最初の１歩であり、そしてすべてのカギを握っている最重要ポイントです。
「相似」が苦手なお子さんを指導することはたくさんあります。
そういうお子さんの多くに共通している弱点が、図形の中に相似形を見つけられない、ということです。
そういったお子さんには、まずは相似形を見つけてごらん、というところからスタートしなくてはいけません。

それでは、実際にちょっとやってみましょう！
あ、でもちょっと待ってください！
その前に、まずは探すべき相似形について、確認しましょう。
探す相手が何なのかもわからずに、それを探すなんてことはできませんからね。
では、あらためて、まずは基本の相似形の確認から。
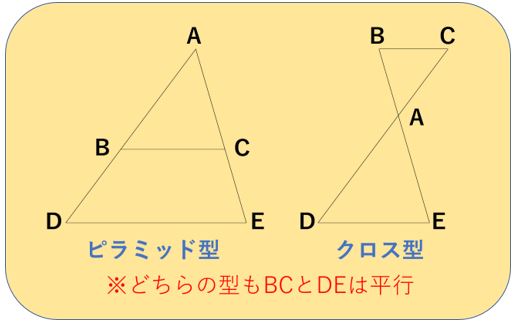
絶対に知ってなければいけない、基本の相似形は以下のふたつです。
呼び名は色々ありますが、ここでは「ピラミッド型」と「クロス型」としておきます。

このふたつが、探すべきターゲットです。
ほとんどの問題が、このふたつの形の組み合わせで解けるようになっています。
まずは、このふたつをよーく頭に刻み込んでください。
ここで一番大切なことは、「BCとDEは平行」という一文です。
もし、この２辺が平行でなかったら、ピラミッドもクロスも、相似形にはなりません。
平行だから「相似」なのです。
平行線は相似形を生む！
この言葉をぜひ覚えておいてください。

それでは、今度はこのふたつをもう少し複雑な図形の中から見つけてみてください。
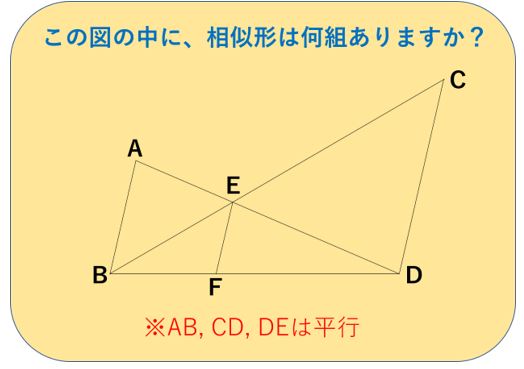
まずはこれです。
平行線に注目にしてくださいね！
平行線は相似形を生む、です！

さあ、どうでしょう？
何組見つけることができましたか？
簡単なようですけど、慣れていないと案外できないお子さんが多いところです。
バカにせずに丁寧に確認してみてくださいね。

では、正解です。
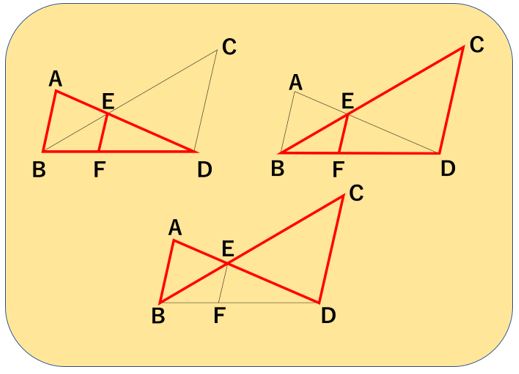
答えは３組ですね。
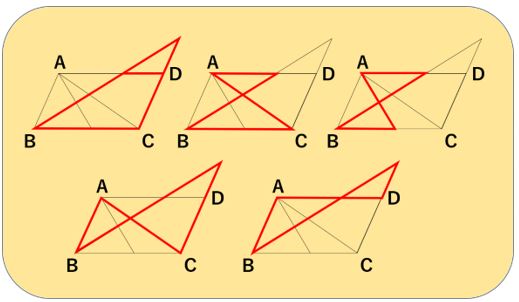
以下のような、３組が見つけられましたか？

最初のうちは、線でなぞってみても構いません。
マーカーとかで目立たせてみてもいいでしょう。
慣れてくると、なにもしてなくても相似形が浮かび上がって見えるようになってきます。
そうなれば、OKです。

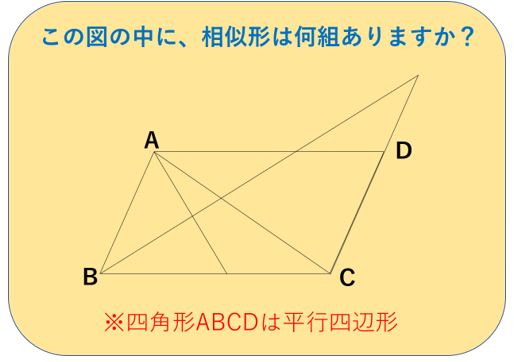
では、次はもうちょっと複雑な図形ですね。
でもこれも、テキストを開けばしょっちゅう出くわすことになる典型図です。
さあ、いったい何組の相似形が隠れているでしょうか？

どうですか？
たくさん見つかりましたか？
これも、ポイントは平行線です。
四角形ABCDは平行四辺形と書いてありますね？
だから、ABとDC、ADとBCはもちろんそれぞれ平行です。
そうすると、あちこち相似形が見えてきませんか？
答えは、５組ですね！

どうでしょう？
ちゃんとこの５組を発見できていましたか？

もちろん、こんな問題は入試でも模試でも出題されません。
実際には、こういう図の中で、長さを求めたり、面積を考えたりします。
しかし、そもそも相似形が見つけられないのに、長さや面積を考えることなんてできませんよね？
どうも「相似」が苦手なんだよなーというお子さんには、まずはこういった練習からしてあげるべきなのです。

これならお家でも簡単に練習ができますよ。
適当にテキストを開いて、「この図形の中に何組の相似形がある？」と聞けばいいのです。
あるいは、ノートに適当に図を書いてあげて、同じことを聞くでも大丈夫です。
大人も一緒に探してあげれば、それOKです。
案外、大人の方が見逃していたものを、お子さんは発見していた、なんてこともあるかもしれませんよ。
ぜひやってみてください。
それでは、また次回お会いしましょう！