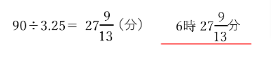みなさん、こんにちは。
受験Dｒ．の坂井智則です。

今回も時計算のおはなし。
内容は前々回のお話の再考です。

前々回に扱った問題を別のアプローチで説明します。
前々回は「まともに解くとこんな感じ」といった方法でしたが、
今回はもう少し発展的な考え方を用いて再考してみることにします。
まともに解く方法は前々回のブログをご参照ください。

扱った問題はこんな問題でした。

【（1）の考え方】
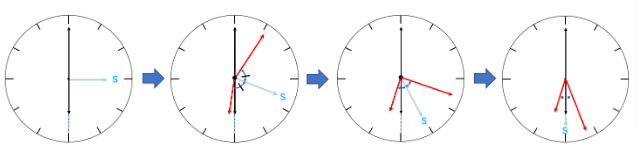
今回は架空の針（シャドー）という考え方を利用していきます。
つねに、長針の方向と短針の方向の真ん中に位置するような針Sを考え、針Sと6時の方向を指す時刻を求めればよいという考え方です。

針Sは長針（＝毎分6度）と短針（＝毎分0.5度）の平均の速さで回転するので、毎分3.25度。

よって針Sが6時の方向を指す時刻は

となります。

【（2）の考え方】
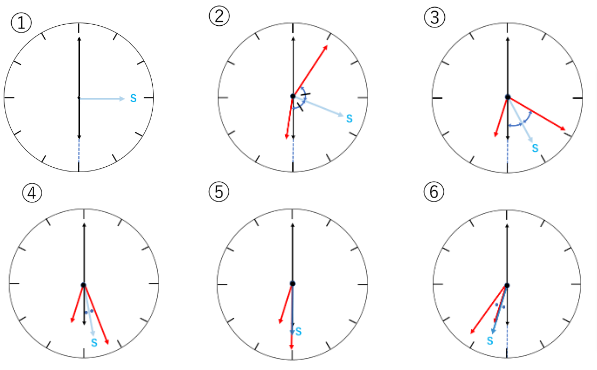
（1）と同様にシャドーを利用して考えます。
つねに、長針の方向と6時の方向の真ん中に位置するような針Sを考え,
針Sと短針が重なる時刻を求めます。

針Sは長針の半分の速さで回転するので毎分3度。（短針は0.5度）
針Sと短針との開いている角度は最初（6時00分の時点）90度だから、重なるのは

となります。

(1)(2)ともまともに解く方法よりかなり簡単に考えることができたのではないでしょうか。
ぜひ試してみてください。

もう1題、今度は長針、短針だけではなく秒針も取り入れた問題にチャレンジしてみましょう
こんな問題です。

【チャレンジ問題】
5時ちょうどから30秒間に、図のように秒針が、長針と短針の作る角度
を2等分するのは、5時ちょうどから何分後ですか。

 
【考え方】
これもシャドーを利用して考えていきましょう。
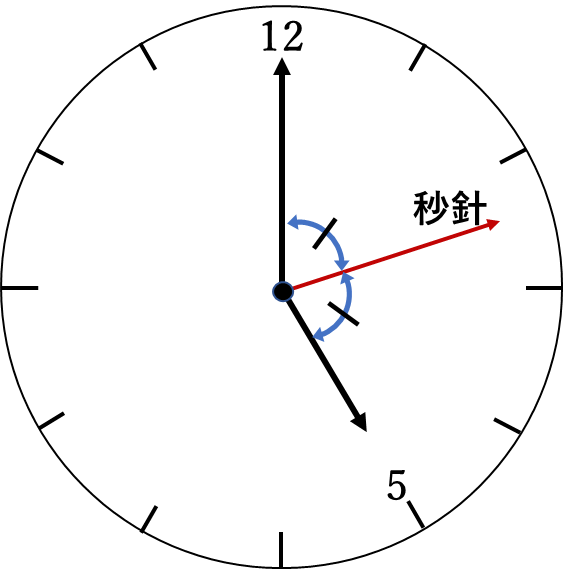
つねに長針と短針の真ん中に位置するような針Sを考え、これと秒針が重なる時刻を求めます。
針Sは毎分3.25度、秒針は毎分360度です。
5時00分の針Sと秒針の開きは75度だから、

今回はシャドーを利用して考えました。
使い慣れれば発展的な時計算の問題も簡単に考えることができます。
ぜひ練習して時計算を得意分野にできるようチャレンジしてみてください。

それでは、またお会いしましょう。