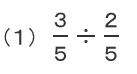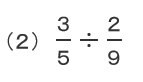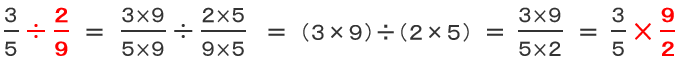みなさん、こんにちは。　海田真凜です。

 

前回のブログが ９/１

今回のブログが ９/４

 

３日前に書いたばかりなのに

再び登場。

 

え、早くない？

なんで？

 

それはですね

 

一時期、ブログをずーっと更新せずにいたら・・・

 

「結構楽しみにしているから、早く書いて」

というリクエストにも応えずにいたら・・・

 

どこからか “海田失踪説”　が流れまして。

卒塾した生徒たちからも

「先生、生きてる？」

と連絡がある始末。

 

また失踪したとか囁かれたくないので

間髪入れずに登場してみたというわけです。

 

 

はい、前振りはここまで。

それではいきましょう。

 

今回のお題は

「わり算の意味、ちゃんとわかっていますか？」

 

 

事の発端は、とあるご家庭からのご相談。

 

何やら、学校の宿題で

「分数のわり算は、なぜ上下をひっくりかえしてかけるのか」　

を説明しなければならないと。

 

中学受験の算数において

その説明をしてもらう機会はほとんどないでしょう。

 

疑問を感じる生徒がいたとしても

そうやって計算するものだと教わって

分数のわり算の授業はおしまい。

 

でも、「わり算の意味」を再確認してもらうには良い題材なので

今回取り上げます。

 

 

＜　わり算を初めて学習したとき　＞

 

初めてわり算を習ったとき

どんな題材を扱ったか覚えていますか？

「６まいのカードを太郎くんと次郎くんで

同じまい数ずつ分けたら、太郎くんは何まいもらえますか」

 

「１５個のボールを３つの袋に同じ個数ずつ入れると

1つの袋に何個のボールが入りますか」

 

このような問題を取り扱うことが多いですね。

 

注目すべきところは

“等しく分ける”　

という点。

 

わり算を初めて学習したお子さんは

わり算　＝　“等しく分ける”　

という意識を持ちます。

 

 

＜　分数を初めて学習したとき　＞

 

さらに、初めて分数を習ったとき

どんな題材を扱ったか覚えていますか？

ピザを６等分した図を用いて

 

 

そんな解説をされたかと思います。

 

ここでも、注目すべきところは

“等しく分ける”　

という点。

 

分数を初めて学習したお子さんは

分数　＝　“いくつかに等しく分けたうちの何個分”　

という意識を持ちます。

 

 

＜　わり算の意味　＞

 

では、わり算の意味は

 “等しく分ける” ということなのでしょうか。

 

実は、その意味は

数の世界が整数のときだけに限られます。

 

でも、ほとんどのお子さんは

分数のわり算を学習するときに

わり算　＝　“等しく分ける”　

と思っています。

 

これが混乱のもと。

 

さらに、分数についても

分数　＝　“いくつかに等しく分けたうちの何個分”　

と思っていますから

どうしても “等しく分ける” という感覚に引きずられます。

 

 

ここで思い出してほしいのが

わり算を学習する前に、必ずかけ算を学習するということです。

 

そこに、わり算の意味を理解するヒントが隠されています。

 

かけ算は

２倍、３倍、４倍、５倍、・・・

というように

２つの数量を比べて

倍数関係でとらえていきます。

 

ここから、わり算の意味は

２つの数量を比べたときに、何倍になっているかを求める

ととらえることができます。

 

数の世界が整数だけでなく

分数に広がった場合には

 

わり算　＝　“何倍かを求める”　

ととらえて下さい。

 

 

＜　分数のわり算　＞

 

さきほどの、学校の宿題に戻りましょう。

 

「分数のわり算は、なぜ上下をひっくりかえしてかけるのか」　

 

２つのわり算で考えてみます。

 

この場合は分母が等しいので

３は２の何倍か、と考えることができます。

 

この場合は分母が異なるため

（１）のように同じ分母にすれば

分子だけを比べて、何倍かを求めることができます。

 

そこで、通分してから、何倍かを求めてみると

結果的に、ひっくりかえしてかけていることになりますね。

 

 

宿題の答え

「分数のわり算は、なぜ上下をひっくりかえしてかけるのか」　

⇒ ２つの分数を比べて、わられる数がわる数の何倍かを求めると

　　  結果的に、ひっくりかえしてかけることになる

 

はい、完成。

 

それでは、また３日後に！

 

と言いたいところですが、もうネタ切れ。

またいつもの順番で登場します・・・。