みなさんこんにちは、受験Dr.の久米です。
今回は算数が苦手なお子さんのために、サイコロ問題を表で解く方法をお伝えします。
中学受験で出てくるサイコロ問題は、2個または3個の場合がほとんどです。
サイコロ2個問題の解き方については、以前書いたこちらをご覧ください。
今回は前回に引き続き、サイコロ3個問題を表で解く方法をお伝えします。

 

サイコロ問題で表整理を使うことのメリットはなんといっても「見やすさ」です。
もう一つのメリットは、書きこんで調べていくうちに法則が発見できることです。
具体的な数字を調べていくうちに場合分けが自然にできます。
「模範解答の式を見ても何のことかわからない」
「場合分けのやり方がうまく行かない」
そういうお子さんは、以下で解説する表整理の方法を取り入れてみてください。

例題1（渋谷教育学園渋谷2020）
A君、B君、C君の3人がサイコロを1つずつ投げたところ、A君とB君の出た目の積は4の倍数で、
B君とC君の出た目の積は9の倍数でした。このような目の出方の組は何通りありますか。

 

前回はサイコロ3個の問題を表6個書くやり方で解きました。
今回はサイコロ3個の問題を表1つにまとめて書くやり方で解いていきます。
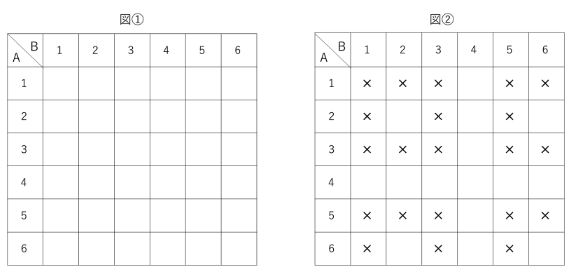
まず、A君とB君のサイコロの目の数を表にします（図①）。
次に、「A君とB君の出た目の積が4の倍数」という条件に合わないところに×を入れます（図②）。
「奇数×奇数」「奇数×2」「奇数×6」は✕となります。

 

次に、✕以外のところで、「B君とC君の出た目の積が9の倍数」になる条件を調べます。
例えば、A2×B2の箇所は、Cがどの目になってもB×C＝9の倍数にならないので✕ですが、
A4×B3の場所は、Cが3または6の場合に条件を満たします。
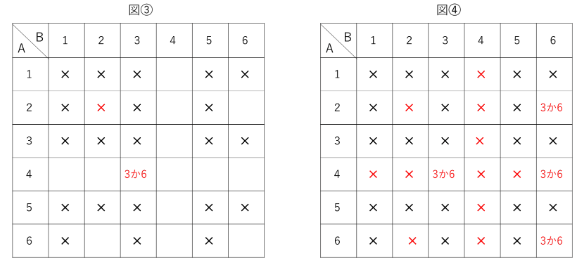
これを図に書きこみます（図③）。
そして全ての空欄を書きこむと、下の図➃のようになります。

 

 

したがって、例題1の答えは8通りです。
この問題のポイントは、A×BとB×Cの条件が違うので、表が対称にならないことです。
丁寧に調べ上げていきましょう。

例題2（渋谷教育学園渋谷2021）
大・中・小3個のサイコロがあります。この3つのサイコロを同時に投げ、出る目の積を考えます。
⑴3の倍数になる目の出方は何通りになりますか。
⑵4の倍数になる目の出方は何通りになりますか。
⑶6の倍数になる目の出方は何通りになりますか。

⑴「3の倍数になる目の出方は何通りになりますか」
例題1と同様に、まず大中のサイコロの目の出方を表で書き、当てはまるところを調べていきます。
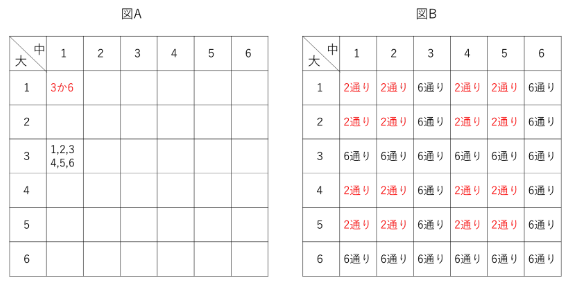
例えば、大1×中1の箇所は、小が3または6の場合に条件を満たします。
大1×中3の場合は、小がどんな数でも条件を満たします（図A）。
調べていくと、どちらも３の倍数でない場合は2通り、
どちらかが3の倍数である場合は6通りになることに気がつくでしょう。
これを表にまとめると、図Bのようになります。

 

 

したがって、⑴の答えは、2通り×16+6通り×20＝156通り

⑵「4の倍数になる目の出方は何通りになりますか」
例題1と似た問題です。
表を書いて調べていくうちに、大と中の出た目が
①「奇数×奇数」②「奇数×（2、6）」③「奇数×4」➃「（2，6）×（2，6）」で場合分けできることに気がつきます。
①「奇数×奇数」⇒小が４のときに条件を満たすので1通り
②「奇数×（2、6）」⇒小が２、４、６のときに条件を満たすので３通り
③「どちらかに4が入る」⇒小はどんな数でもOKなので６通り
➃「（2，6）×（2，6）」⇒小はどんな数でもOKなので６通り
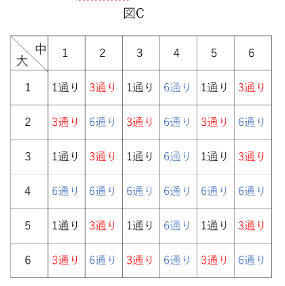
以上を表に書きこむと、図Cのようになります。

 

 

したがって、⑵の答えは、1通り×9+3通り×12+6通り×15=135通りとなります。

⑶「6の倍数になる目の出方は何通りになりますか」
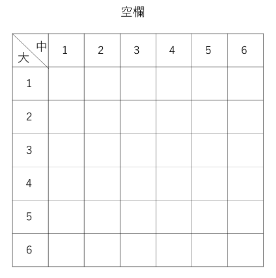
⑶については、下の空欄の表を使って、お子さん自身でチャレンジしてみてください。

 

 

それでは解答です。
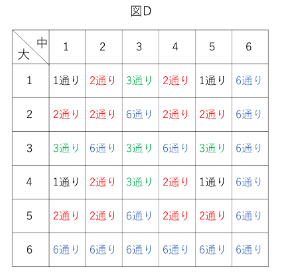
表に書きこむと下の図Dのようになります。

 

 

したがって、⑶の答えは1通り×4+2通り×12+3通り×5+6通り×15=133通りとなります。

場合分けのやり方がよくわからないお子さんは、
サイコロ問題の表整理の方法、ぜひ使ってみて下さい。

それではまた。受験Dr.、久米でした。