みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。
塾に通い、中学入試を目指す皆さんは新学年になりましたね。
あと1年という期間を一生懸命過ごし、志望校合格に向けて頑張りましょう!
さて、本日はタイトルの通り、誘導形式の問題について触れたいと思います。
単元学習が一段落した子も多いと思います。
実戦形式の問題の面白さや奥深さを感じ取っていただければ幸いです。
問題がやや長いですが、是非最後までお付き合いください。
図2は一辺の長さが1の立方体を4個組み合わせて、横幅4、高さ1、奥行き1の直方体を作り、その直方体と点A、Bを結ぶ道をつけたものです。図1と同じく太線で表された道を通ることができます。
これらの道を右、上、または奥のいずれかに進むことで、点Aから点Bまで移動するとき、考えられる移動経路はそれぞれ何通りありますか。(開成2019)
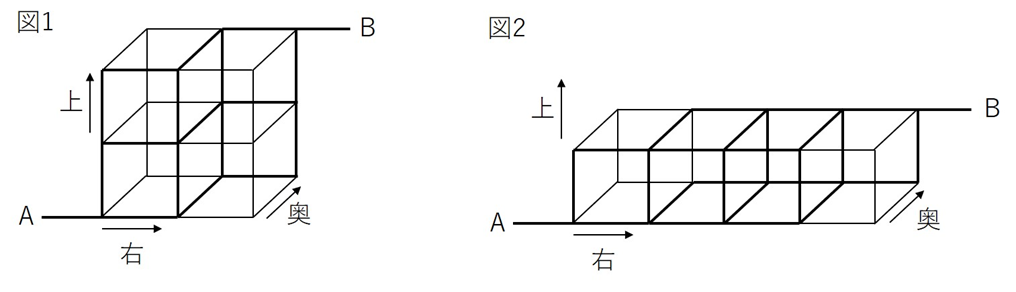
空間内の道順の問題です。スタート地点と同じ平面にある面から埋めていき、丁寧に作業をすれば解答までたどり着けます。
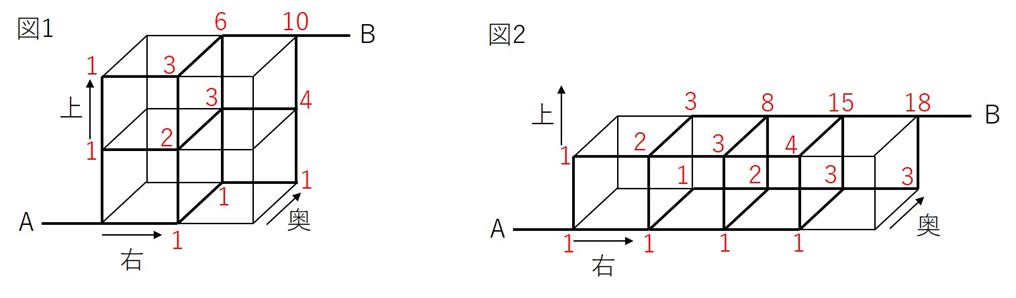
より、図1は10通り、図2は18通りとなります。
ここからが本番です。
(2)図3は一辺の長さが1の正方形を2個並べて横1、 縦2の長方形をつくり、
その長方形と点A、Bを結ぶ道をつけたものです。
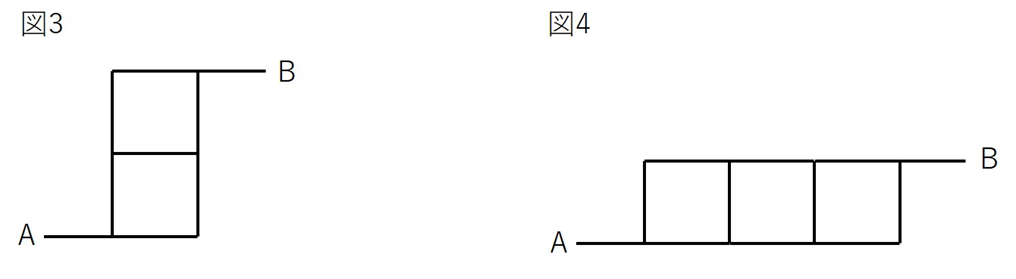
図の中で点Aと点Bを結ぶすべての線が、通ることのできる道です。
図4は一辺の長さが1の正方形を3個並べて、横3、縦1の長方形をつくり、
その長方形と点A、Bを結ぶ道をつけたもので、それぞれ図1と同じく点A、Bを結ぶすべての線を道として通ることができます。
次のような規則に従ってこれらの道を通り、点Aから点Bまで移動することを考えます。
【規則】
「一回だけ左に1進み、それ以外は右または上に進む」
ただし、進む方向を変更できるのは正方形の頂点の場所だけです。
点Aにもどったり、点Bからもどったりはできません。
また、規則に従うかぎり、同じ道を2回以上通ることも可能です。
このとき、図3の点Aから点Bまでの移動経路は10 通りあります。
では、図4において考えられる移動経路は何通りありますか。(一部省略)
通常の道順の問題であれば、(1)と同様の作業で解くことができますが、与えられた規則がこの問題を難しくしています。「1回だけ左に進む」という操作によって、どのように整理していけばよいかわからなくなった受験生もいたのではないでしょうか。
一方で、この問題を一瞬で解いた子もいるはずです。
(1)の解答と、(2)のリード文を見比べ、何か気付くことは無いでしょうか。
そう、図1の解答と、図3の解答が同じだということです。
こういった気付きは、上位校を目指すうえで非常に大切な要素です。
果たしてこれは偶然なのでしょうか。
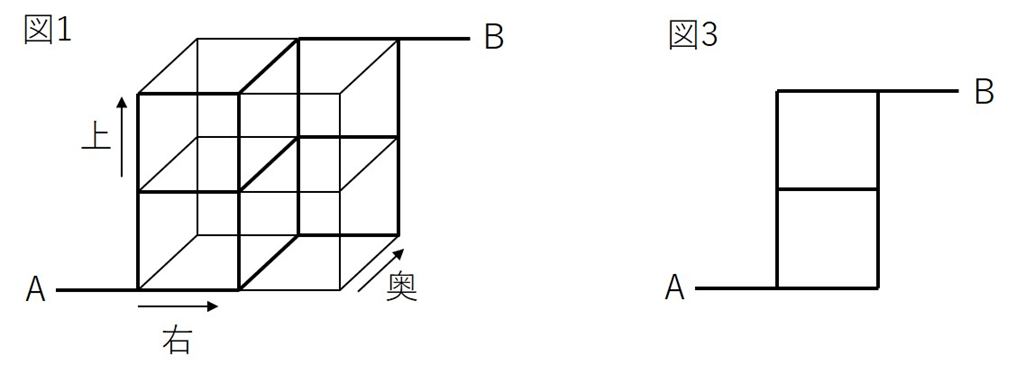
一見、図1と図3は全く別の図に思えます。
ここで、(2)で与えられた規則を思い出してみてください。
【規則】
「一回だけ左に1進み、それ以外は右または上に進む」
「図3において1回だけ左に進む」という操作は「図1において奥に進む」操作と同じになっていることに気付きませんか?
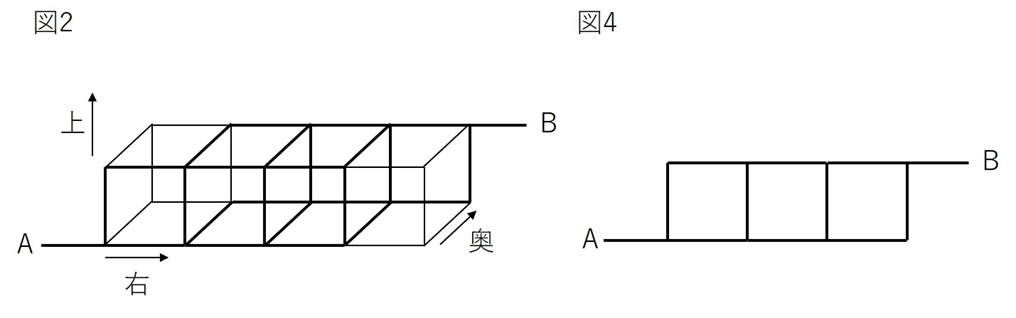
図2と図4も、本質は全く同じです。
図4の答えは図2と同じく18通りとなります。
誘導形式の問題を解くためには、「気付き」や「ひらめき」が不可欠です。
初めて見る問題や、難しい問題に対して粘り強く考える習慣をつけ、来年の入試で最高の結果を出しましょう!




