みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。

2020年もいよいよ終わり、2月1日まで、あと1ヶ月となりました。
悔いの残らないよう、残りの期間を精いっぱいやりきりましょう！

さて、今回はタイトルにもある通り、倍数判定法のお話です。

まずは基本知識の確認です。

おそらく皆さんしっかり覚えていることと思います。
しかし、理由まで完璧に説明できるでしょうか。
特に3の倍数です。

3桁の整数ABCについて考えます。
（Aは100の位の数、Bは10の位の数、Cは1の位の数です）
各位の数の和、つまりA＋B＋Cの値が3の倍数であれば
3桁の整数ABCが3の倍数になっていることを示します。

以下証明です。

3桁の整数ABCは、以下のようにあらわすことが出来ます。

100×A＋10×B＋1×C

式を変形します。
100×A＋10×B＋1×C
＝99×A＋1×A＋9×B＋1×B＋1×C
＝99×A＋9×B＋A＋B＋C

99×A、9×Bは3の倍数、かつA＋B＋Cも3の倍数なので
3桁の整数ABCは3の倍数である。

式を変形することで、3の倍数の判定法の理由を説明することが出来ました。

さて、ここからが本番です。まずは問題です。

13の倍数判定法を知っている子は少数でしょう。

ここで、タイトルにもある7×11×13が役立ちます。

ちなみに、7×11×13＝1001です。

ここでひらめいた子もいるかもしれませんね。

それでは式変形を行います。

2□01□5 ＝ 2□0×1000＋1□5
＝ 2□0×1001－2□0＋1□5
＝ 2□0×1001－(2□0－1□5)

3の倍数の判定法で触れた式変形との共通点を感じてもらえると嬉しいです。
1001は13の倍数なので、かっこの中の2□0－1□5が13の倍数であればよいわけですね。
筆算の形にして考えてみます。

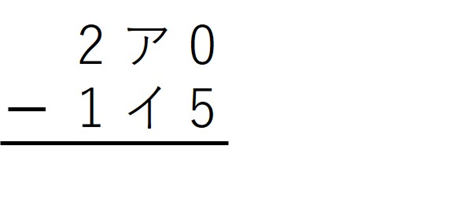
この答えが13の倍数になればよいわけです。
もう気付いた子が多いのではないでしょうか。計算結果の1の位は5になります。
1の位が5になる13の倍数は65です。
（195も一応候補ですが、ア＝9、イ＝0でも計算結果は185です。195になることはありません。）

よって（ア，イ）＝（0，3）、（1，4）、（2，5）、・・・・（6，9）の7個が答えとなります。

1001ってとても便利です。（999も便利だけど・・・）

ちなみにもう皆さん、これで7の倍数や11の倍数の判定も出来ますね！

昨今の入試問題では、冒頭で確認した倍数判定法を覚えているだけで解ける問題が少なくなっているように思います。
倍数判定法をただ覚えるのではなく、「何故そうなるのか」という疑問を大切にしてください。

それでは、失礼します。