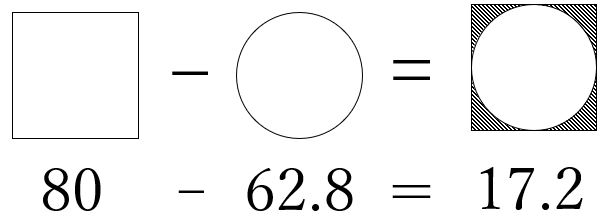こんにちは、受験ドクターのK.Dです！

6年生の方は受験当日まであと4ヶ月ですね。

ここで今一度、「半径の分からない円の面積」の求め方を確認しておきましょう。
ポイントは「半径ではなく半径×半径の値を求めること」です。

では、早速ですが、問題にいきましょう。

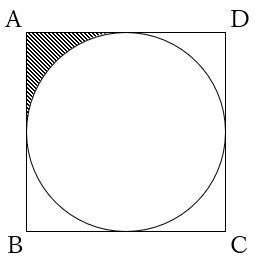
問　下の図のように正方形ABCDの中に円が入っている図形があります。正方形ABCDの面積が80㎠のとき、斜線部分の面積を求めなさい。ただし円周率を3.14とします。

いかがでしょうか。解けた人は一番下までスクロールしてください。
ではヒントを出します。

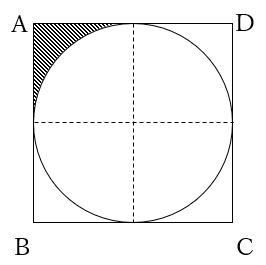
ヒント：正方形の面積＝1辺×1辺で、この図において正方形の1辺は円の直径になっていることに着目しましょう。

正方形の1辺は円の直径になっているので、正方形の1辺×1辺＝円の直径×直径です。
正方形の面積は80㎠なので、正方形の1辺を□㎝とすると、□×□＝80
よって、直径×直径＝80
すると半径×半径も分かります。

＜答え＞　
直径×直径＝80なので、半径×半径＝（直径÷2）×（直径÷2）＝直径÷4＝20となります。
よってこの円の面積は20×3.14＝62.8（㎠）
斜線部分の面積は正方形から円の面積を引いたものの1/4なので、
（80－62.8）÷4
＝17.2÷4
＝4.3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答え　4.3㎠

今後も受験までに確認しておきたい問題を紹介していくのでぜひご活用ください！