受験ドクター算数科のI.Sです。

約数や倍数の問題で、とても便利なのが「ベン図」です。

塾で教わる際には「ベン図は便利だからかこうね！」と必ずと言っていいほど言われると思います。

 

しかし、次第にベン図を書かなくなる生徒がいます。

なぜでしょうか？

書かなくても大丈夫なのでしょうか？

結論は「書いた方がいい」です。

 

図を描いた方が良いと、きっと塾の先生もお父さまお母さまも言っているでしょうに、それでも省略したがる生徒が多いのです。

 

今回のブログでは、ベン図をかいた方が良い理由を説明していきます。

お子様から「どうして図をかいた方がいいの？」と聞かれた際にうまくこたえられるように、準備しておきましょう！

 

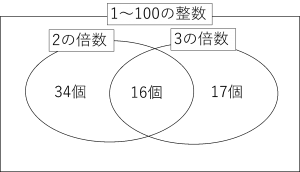
まず、一般的にベン図が有効だとされている問題には次のようなものがあります。

 

 

この問題では、下のような図をかくことが推奨されます。

しかし段々と生徒の理解が進んでくるとこんな風に言うようになります。

「50と33を足して16を引くと67。だから100-67で答えは33だ！　図なんて書かなくても簡単だよ！」

 

小学生というものは、とかく図を省略したがります。

本当にいいのでしょうか？
もう一度結論を書いておきますが、ダメです。

 

それではもうひとつ例題を出してみます。

 

 

どうでしょうか。2と3と5の倍数を調べないといけません。
このくらい複雑にすれば、さすがに生徒も図の重要性を分かってくれるだろう……と思っていると。

 

「はーい先生！　足して、引いて、最後に足すやつでしょ！」

 

のようにアッサリ解いてしまったりします。

頻出問題ですので、解法を覚えている子が多いのです。

この生徒が一体何を言っているのか、簡単に解説します。

 

まず、1から100までの間に2・3・5の倍数、2と3、2と5、3と5、2と3と5の公倍数がいくつあるのかを計算します。

 

100÷2＝50

100÷3=33・・・1

100÷5=20

100÷6=16・・・4

100÷10=10

100÷15=6・・・10

100÷30=3・・・10

 

とここまで計算しておいて

50+33+20-（16+10+6）-3＝74

100-74=26

よって答えは26　だという計算をしています。

 

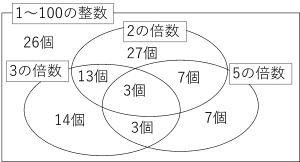
ベン図にすると下のようになります。

小学6年生になると、ここまでの手順を一挙動でパターン化して暗記している生徒もいます。

もはや図を書かずとも「前に解いたあの問題だ。もうすっかり覚えてしまったよ。足して引いて足して……」

のようにパターン化して考えています。

 

さて、ここまでパターン化して暗記できるなら、ベン図は書かなくても良いのでしょうか？
結論は変わりません。ダメです。

 

この問題は確かにパターン化で解けるのですが、一転してよく似た別の問題では間違えやすくなってしまいます。

 

入試問題を作成する中学校の先生たちも、受験生がこの手の問題の解法を暗記しているだろうということは重々承知しています。

そのうえで、少しひねった問題を出すことにより「ちゃんとベン図を描いて整理できるかな？」というところを聞いてきます。

 

例えば次のような問題

 

このような問題で

「ふむふむ、これもきっと例のやつだな。足して引いて足せばいいんだ。50+33+20-（16+10+6）+3＝74だ！」

 

という誤答が出ます。

この問題は「黒い面が上になっているカードの枚数」つまり、「ひっくり返した回数が奇数回」ということです。2回ひっくり返したカードは再び白い面が上になっているので、求める数に含まれません。
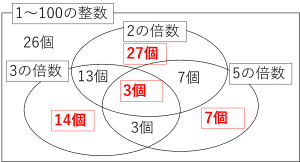
このことを念頭にベン図をかくと、

図の色を付けた部分が、奇数回ひっくり返したカードになります。

ベン図を描いていれば、答えを出すのは簡単ですよね。

 

27+14+7+3=51　です。

 

このように、入試では「見たことありそうな問題だけどいつもとちょっと違う」という問題が出題されます。（難関校では更に複雑な問題文になって出題されます）

その際にはベン図などの図をかいて問題を整理することが必要です。

 

普段から「またあのパターンだ」と過度に省略してしまっていると、いざ応用問題に直面した際に手が出しにくくなります。

ベン図を描き慣れておくことで、テストや入試本番で手が動くようになります。

時には地道な方法も、練習しておきましょう。

 

やみくもに「かきなさい！」といっても小学生はなかなか言うことを聞きませんので、図をかく必要性や有効性を分かりやすく示してあげることが大切になります。

 

それではまた！