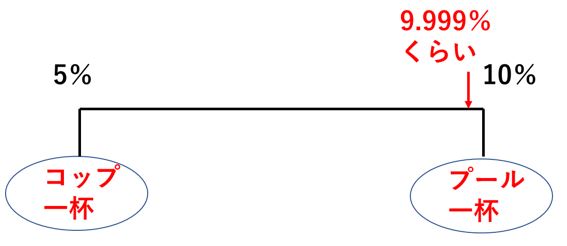こんにちは。受験ドクターのI.Sです。

食塩水の濃度の問題で、てんびんの図を描いて求める方法をご存じでしょうか。
濃度計算は、面積図を用いる解法を最初に習うことが多いようですが、入試に向けて、てんびん図というものを使えると少し有利になります。
今日はこのてんびんの考え方をどのように指導するのが良いのか、一例をご紹介します。

慣れ親しんだ面積図方式から移行することにリスクを感じてらっしゃる方も、意外と簡単だと思っていただけたら嬉しく思います。

まず、5％の食塩水Aと10%の食塩水Bを混ぜる状況を考えます。すると、何％になるでしょうか？当然ですが、5％から10%の間になりますよね。

混ぜて何％になるかは、AとBの量によって変わります。
では、次のような極端な例を考えてみましょう。

5%の食塩水をコップ一杯分、10%の食塩水をプール一杯分混ぜます。
どうなるでしょうか？多少は薄まりますが、ほぼ10%のまま変わりませんよね。感覚的に、多分9.999%くらいになると思います。

上の図のように、数直線の、限りなく10%に近いが少しだけずれたところ、の値になります。
これを利用して、てんびんを描いてみます。

5%と10%の数直線をてんびんの棒に見立て、左端と右端に、それぞれの水溶液と同じ重さのおもりを吊るします。
コップとプールの重さを釣り合わせるためには、支点はかなり右寄りになります。この支点の位置が、混ぜた際の濃度を表しています。
つまり、左と右に吊るしたおもりの重さによって、釣り合う位置がずれていくのです。次に具体的な数値で見ていきましょう。

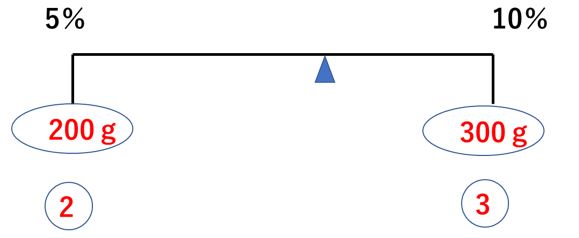
5%の食塩水を200ｇ、10%の食塩水を300ｇ混ぜると、何パーセントになるでしょうか？　という問題を考えます。
これもてんびんの図で考えていきます。図のように、10%食塩水の方が重いので、釣り合う支点の位置は真ん中よりも右寄りです。
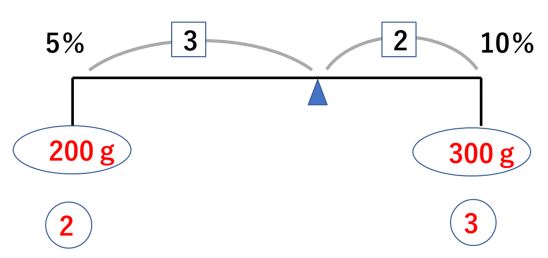
では、どの位右寄りなのでしょうか？　これは食塩水の重さの比に関係します。
重さの比が2：3になっています。ですので、下の図のように

てんびんの長さの比は3：2になります。
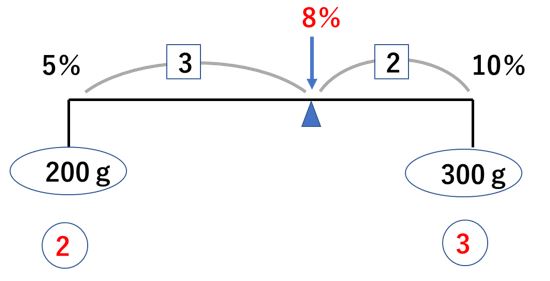
混ぜたときの濃度は支点の位置になりますので

このように、8パーセントだと分かります。

いかがでしたでしょうか。
長く面積図に親しんできた生徒にとって、濃度の問題を解くときになぜてんびんの図が登場するのか、最初は
理解しづらいかもしれません。
もちろん、どこにどの数字を書き入れるのかを暗記させて、システマチックに処理させる方法もあるでしょう。
しかし、それでは面白くありません。せっかく勉強するのですから、どうしててんびんの図で濃度が求められるのか、実感として掴んでもらいたいです。
そのための導入方法の一つとして、プール一杯という極端な数値設定で説明する例をご紹介しました。
このように極端な数値を用いる方法はほんの一例で、算数の様々な単元・解法について、子供が理解しやすい説明のためのテクニックがあります。
算数を嫌いにさせないため、身近なものとして捉えてもらうため、うまく導入してあげることで、拒否感なく受け打入れてくれます。
是非ご家庭で食塩水問題を指導される際の参考にしてみてください！