みなさん、こんにちは。
受験ドクター　理科・算数担当のT.H.です。

2月1日からの都内入試をひかえて、受験生の皆さんは復習に専念していることと思います。
この時期に理科は何をするかというと、もちろん過去問の復習をすべき…
なのですが、埼玉・千葉などで入試を受けてきた人は、時事問題の出題内容にも気を配りましょう。

それが終わった人は、志望校の頻出単元を強化していきましょう。
自信をもって解ける単元が1つ増えるだけでも、だいぶ前向きに受験に挑めますよ。

というわけで、最頻出単元の中和計算をつづけていきたいと思います。
今回は中和した後に残った固体の重さを求める方法について考えてみます。

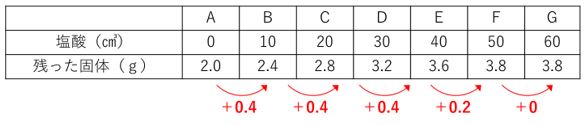
問　　水酸化ナトリウム水溶液50㎤に様々な量の塩酸を加え、A～Gのビーカーをつくりました。できた水溶液を蒸発させて残った固体の重さを量り、表にしました。

塩酸を30㎤加えた場合、できた食塩の重さを求めなさい。
ただし答えは四捨五入して、小数第一位までで答えること。

前回と同様、化学計算の表があったら「差」を書き込んでおきます。

このパターンの注意点は、はじめから水溶液に水酸化ナトリウムが入っていることです。
水酸化ナトリウムは固体なので、はじめのＡのビーカーが0ｇからスタートになりません。
単純な比例計算ではないことに注意しましょう。

差を見ると、ＥとＦのあいだで完全中和していることがわかります。
塩酸10㎤あたりで固体が0.4ｇずつ増えているので、この増加量を使って計算します。
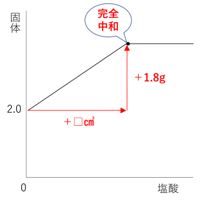
完全中和までに増加した固体の量は
3.8　－2.0　＝　1.8ｇ
10㎤あたりに0.4ｇなので
1.8　÷　0.4　＝4.5倍
中和に必要な塩酸の量は
10 × 4.5 = 45㎤　　とわかります。

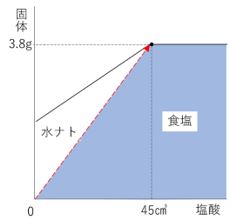
グラフにすると下図のようになります。

ポイントは、増加量に注目すれば比例が使えるということです。
化学計算は、常に比例を利用して計算していきます。
一見計算不可能なようでも、見方を変えれば可能になります。
「比例を見つける」
これを頭に入れて、つぎの計算にいってみましょう。

ではあらためて、本題の固体量計算に入ります。

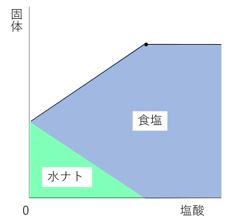
色々な塾教材で見られるように、グラフを色分けします。

完全中和したときに水酸化ナトリウムは0ｇになるはずなので、
右図のようにすると水酸化ナトリウムが一定量ずつ減っている
様子がわかりやすいですね。
固体の重さから水酸化ナトリウムの重さを引けば、食塩の重さ
を求めることができます。

しかしこの解き方、比例っぽくないですね。
水酸化ナトリウムと食塩を区切る線は、引き方が決まっているわけではありません。
食塩の量を出したいなら、食塩優先のグラフに変えてみましょう。

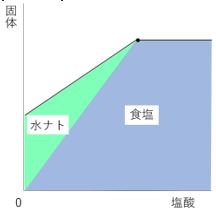
下図のように、水酸化ナトリウムの位置を変えてみました。

完全中和したときに水酸化ナトリウムが0になるので、
さきほどのグラフと数値は変わっていません。

このグラフだとどうでしょう。
水酸化ナトリウムの部分を無視して食塩の部分だけ見てください。
比例のグラフになるのがわかるでしょうか。（右下図）
あとは普通の比例計算です。
塩酸を45㎤加えたときに食塩は3.8ｇあることがわかっているので、
塩酸30㎤に対する食塩の量は

3.8 × = 2.53333…
四捨五入して2.5ｇとなります。

このように一見するとわからないですが、比例がかくれている問題はたくさんあります。
化学単元ではかくれた比例関係を探して、計算を優位にすすめましょう。