みなさん、こんにちは。
受験ドクター算数科の江田です。

前回は
「Ｎ進数」の位取りのしくみ
についてお話しましたね。

今日は実際にN進数の問題に触れてみましょう。

さっそく以下の問題を考えてみてください。

さて、いかがでしょうか。

まずは(1)から。

3進数の「1201」ですから、
たとえば右から2番目の「0」は“10の位”の数ではありません。

そう、前回お話したとおり、
3進数の位取りは10進数とは違って
右の位(一番小さい位)から順に
1の位
1×3＝3の位
3×3＝9の位
9×3＝27の位
と続いていきましたね。

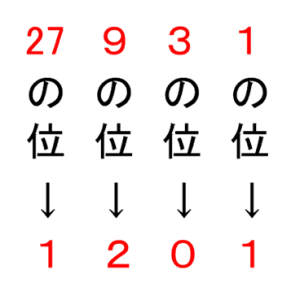
つまり
「1」を表す数が1個と
「3」を表す数が0個と
「9」を表す数が2個と
「27」を表す数が1個
集まった数を表しているのです。

よってこれは我々が普段使っている数字
つまり10進数の
1×1＋3×0＋9×2＋27×1＝46
を表していたということです。

続いて(2)。

こちらは
10進数の「182」を４進数に直します。

１０進数の「182」は
「1が182個集まった数」
です。
これを4進数の世界に持って行くイメージを持ちましょう。

前回お話したとおり、
何進数でも一番小さい位(下の位)は「1の位」です。
つまり、
4進数の世界に持って行っても
「1が182個集まった数」
であることに変わりないのです。

では、ここから
4進数の世界のルール(4進法)にしたがって
くり上がりをしていきましょう。

4進法は
「1つの位に4つの数がたまったら1つ上の位に1くり上がる」
というルールでした。

1の位に182個の数がたまっている状態なので、
まずは
182÷4＝45あまり2
より、
1つ上の位(4の位)に45個の数がくり上がり、
2個の数は1の位に残ります。

さらに
4の位にたまっている45個の数を
さらに上の位にくり上げます。

45÷4＝11あまり1
より、
さらに1つ上の位(4×4＝16の位)に11個の数がくり上がり、
1個の数は4の位に残ります。

同じく、さらに
16の位にたまっている11個の数を
さらに上の位にくり上げます。

11÷4＝2あまり3
より、
さらに1つ上の位(16×4＝64の位)に2個の数がくり上がり、
3個の数は16の位に残ります。

64の位にたまっている2個の数は
これ以上さらに上の位にくり上げることはできませんから、
2個の数が64の位に残ります。

よって、上の位から順に書くと

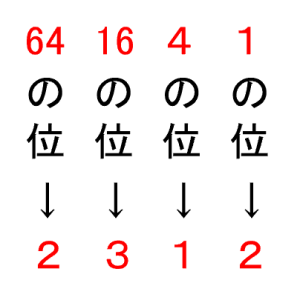
ということになります。
これが4進数で表した数です。

ちなみに今やったことは
「ひたすら4で割って余りも書いて…」という連除法をしていき、
4で割れなくなったところで
下のように一番外側の数字を矢印の向きに書き出す
という作業をすれば求められます。

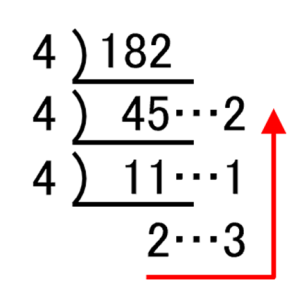
おそらく、
この連除法のかたちが頭に入っている受験生も多いことでしょう。

ただ、
そもそもなぜこの連除法で求められるのか
という根本の理解が伴っていないと、
「あれ？Ｎ進数を10進数に直す方法が連除法だったっけ？」
「10進数をＮ進数に直す方法はどっちだったっけ？」
という混乱につながります。

是非今回の話を参考にしていただき、
このＮ進数の基本の解法を完璧に定着させましょう！

それではまた次回。