みなさん、こんにちは。受験ドクター算数科のA.K講師です。
前回の記事では、今年の入試問題を使って “共通部分”を探して考える平面図形のアプローチ方法をお伝えしました。
今日は、引き続き図形分野における相似形の利用に焦点を置いた考え方をお伝えしましょう。
題して…
「延長線を用いた2組のクロス型相似!」
憶えていますでしょうか?
今年の入試問題にチャレンジ!~図形篇・前篇~の記事において触れた、あの考え方です!
鷗友の問題に続き、今回は神奈川県の大学附属校の代表である慶應普通部の問題にアタックしてみましょう!
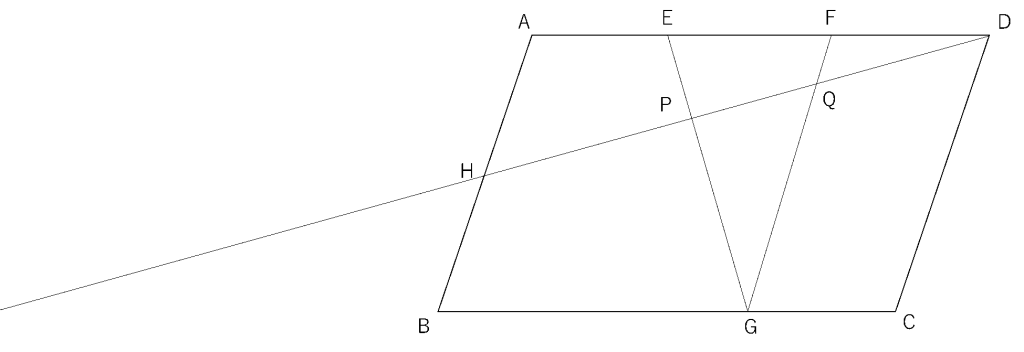
平行四辺形ABCDがあります。ABの真ん中の点はHで、AE=EF=FD=GCです。点P、QはDHとEG、FGの交わった点です。HP:PQ:QDを求めなさい。
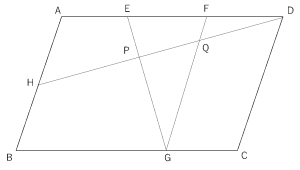
さて。着目するのは、この図形が平行四辺形であること→ADとBCが平行→クロス相似があるんじゃないか?ということです。
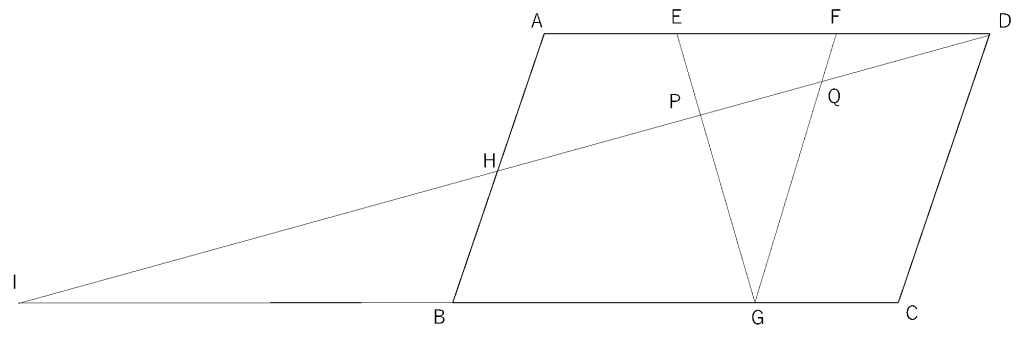
ところが!Dから伸びている線がHで止まってしまって、三角形FQDや三角形EDP、さらには三角形ADHを砂時計相似に活かせない!モヤモヤ感があるそんな時こそ、線を延長して多くのクロス相似を生み出してしまうのです。具体的な手順は以下のようになります…。
①DHをHの外に延長する。
②CBもBの外に延長し、先ほど延長した線との交点をIとする。
③クロス相似をあるだけ見つける。
Ⅰ…三角形ADHと三角形BIH
Ⅱ…三角形DEPと三角形GIP
Ⅲ…三角形DFQと三角形IGQ
なんと2つだけではなく、今日の問題では3つも見つかります!
まずはⅠに着目すると、AH:HB=1:1なのでDH:HI=1:1です。AE=①とおくと、問題文の条件よりEF=FD=GC=①でAD=③となり、Ⅰの相似からADもBIも等しいのでBI=③です。
続いてⅡに着目すると、DE=②、GI=GB+BI=②+③=⑤なのでDP:PI=2:5です。
さらにⅢに着目すると、DF=①、GI=⑤なのでDQ:QI=1:5です。
④これらのことを踏まえ、DIに着目する。
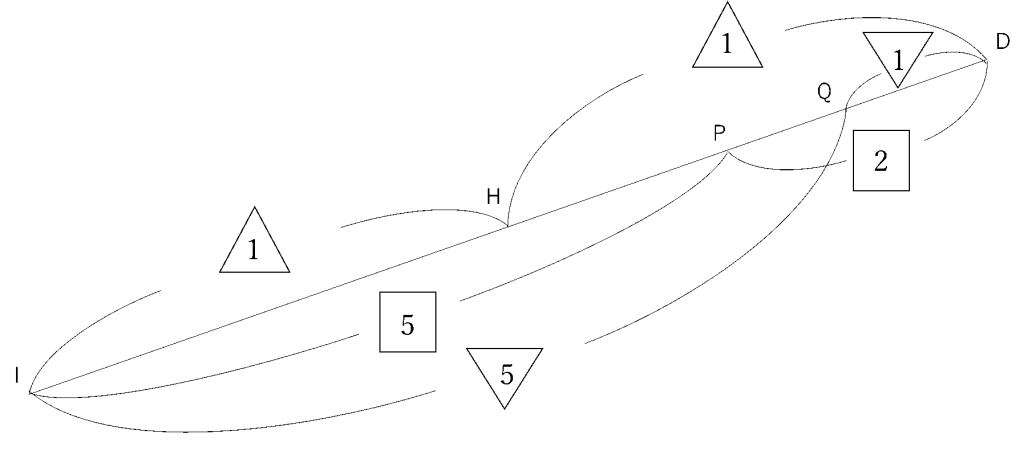
ここで3連比を用いて考えます。DIの長さを1+1=2と5+2=7と5+1=6の最小公倍数である42にそろえると、DH=HI=21、IP=30、PD=12、IQ=35、QD=7となります。
HP=DH-PD=21-12=9、PQ=PD-QD=12-7=5なので求めるべきHP:PQ:QDは9:5:7となります!
なお、クロス相似→3連比を用いないで考える方法も解説として載っているようですので、そちらも参考にして図形の色々なアプローチ法を学んでいってくださいね!
それではこの辺で本日のまとめとしましょう。と言っても、少しだけ鷗友の時のblogとかぶりますが…
~今回のまとめ~
図形の平行線+三角形→線を延長してのクロス相似が出来ないかを試してみる
→相似が3つ以上出来る場合もある
→その場合でも特定の辺に着目して比を揃えるプロセスを踏む。
いかがでしたでしょうか。これで、だいぶクロス相似を作成する問題の考え方に慣れてきたのではないでしょうか?次回は、入試問題から少し離れ、アッと驚く算数の世界をまた披露したいと思います!
ではまた、お会いしましょう♪