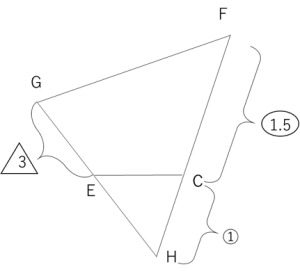みなさん、こんにちは。受験ドクター算数科のA.K講師です。

 

今回の内容は、前回の宿題の答え合わせ＆鷗友の入試問題の後半の答え合わせです！

 

・宿題について

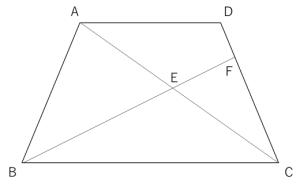
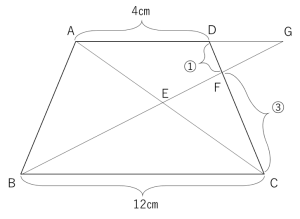
下の図のような台形ABCDがあり、AD=4㎝、BC=12㎝、高さが10㎝です。DF:FC=1:3であるとき、四角形AEFDの面積を求めなさい。

 

 

クロス型の相似がない場合は、線を延長して作ってみましょう！Bから伸びている線が、Fで止まってしまっているのでそのまま延長し、ADの延長線との交点をGとします。以下のようになります。

 

 

ここで、三角形AEGと三角形EBC・三角形DFGと三角形FBCの2組のクロス型相似が出現します！

 

まずはDFGとFBCの相似に着目すると、DF:FC=1:3なのでDG:BCも1:3となり、DG=12×
=4㎝となります。四角形AEFDは特殊な四角形（台形や平行四辺形など）ではなく、直接面積を求めることができないので、三角形AEGから三角形DFGを引けばよいですね。先ほどの相似から、三角形DFGの高さは10×

=2.5㎝となるのでその面積は4×2.5÷2=5㎠となります。

次にAEGとEBCの相似に着目すると、AG:BC=(4+4):12=2:3なので各々の三角形の高さの比も2:3となります。三角形AEGの高さは10×

=4㎝となるので、その面積は8×4÷2=16㎠です。

よって、四角形AEFDは16-5=11㎠となります。

 

では続いて、鷗友の後半の問題の答え合わせといきましょう。

 

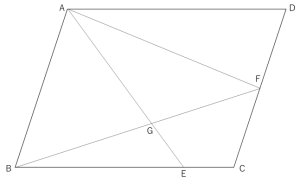
図の四角形ABCDは平行四辺形で、AB:AD=3:4、DF:FC=1:1です。

 

 

(2)三角形AGFと四角形CFGEの面積の比を、最も簡単な整数の比で表しなさい。

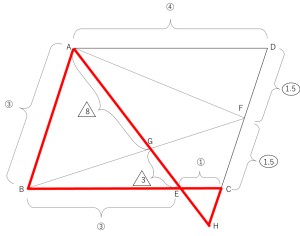
違う図形なので、三角形と四角形をそのまま較べることはできません。まずはFCをCの方へ延長し、またGEをEの方へ延長してお互いの交わった点をHとします。以下のような図となり、新たなクロス型相似が見つかります。

 

 

 

三角形ABEと三角形ECHのクロス型相似から、相似比はBE:EC=3:1で、CH=①となります。

 

 

続いて、三角形ABGと三角形GHFのクロス型相似に着目すると、相似比はAB:FH=3:(1+1.5)=6:5となります。AG:GHも6:5になることを利用すると、高さ一定から三角形AGFと三角形HGFの面積比は6:5となりますので、三角形AGFを、三角形HGFをとします。

次に、三角形HGFに着目します。

 

 

三角形ABEと三角形ECHのクロス型相似から、EH=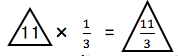と求まります。

EH:GH=：（+3 )=11:20、HC:HF=1:(1+1.5)=2:5となるので、三角形ECHは三角形HGFの×=倍です。ここから、四角形CFGEは

×(1-)=と求まります。

よって、三角形AGFと四角形CFGEの面積比は、：=20:13とわかります！

 

 

いかがでしたでしょうか？鷗友の図形の問題は、決して複雑な手法を用いて答えを求めるような、難易度の高いものではないので、相似が苦手という方は過去問も含めて練習してみてくださいね！

今回はここまでといたします。次回は、さらに今年の入試問題をさらっていきたいと思っています。

 

ではまた、お会いしましょう♪