みなさん、こんにちは！受験ドクター算数科のA.K講師です。

 

今回も、各単元について簡単な例題を交えながら、その考え方をもとに実際の入試問題に挑戦してみましょう。

本日は、文章題の単元の一つである集合算について考えていきます。集合算は、問題文を読みながら、どんな人たちがグループになっているのかを整理することがポイントになります。

さらに、そこに割合も絡んだ複合問題をご紹介していきましょう。

では、例題をここで一つ・・・

 

（例題）

小学校のあるクラスの中に、算数が好きな人は全体の1/2 、国語が好きな男子は全体の1/6 、女子は全体の1/3います。算数が好きな男子が12人いるとき、このクラスの人数は何人ですか。

 

この問題においてまず考えるべきなのは、クラスの中にどんなグループが存在しているか？、ということです。

算数が好きな人、国語が好きな人、男子、女子。４種類のグループがいることがまず分かります。ただ、さらに詳しく見てみると算数が好きな男子・女子、国語が好きな男子・女子と別れますね。

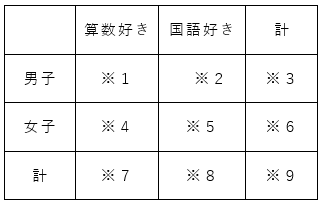
このような時には、下のような表を使って整理してみましょう！

表の各部分について。※１は男子で算数好き、※２は男子で国語好き、※３は男子全員、※４は

女子で算数好き、※５は女子で国語好き、※６は女子全員、※７は算数が好きな人全員、※８は国語が好きな人全員、そして※９は全体の合計なのでクラス全体の人数を示します。

 

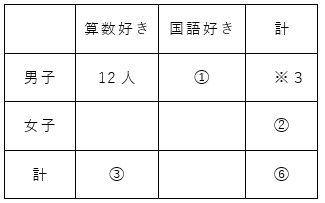
それでは、実際に問題文に従って表を埋めてみましょう。

問題文に分数として与えられている割合の分母がそれぞれ２，６，３なので、最小公倍数をとって全体の人数を⑥とおきます。（表の各部分を整数で出すため）

そうすると、計算した結果が以下のようになります。

ここで、※３の部分は⑥－②＝④となり、算数好きの男子は④－①＝③＝１２人となります。

よって、①＝１２÷３＝４となり、クラスの人数は⑥＝４×６＝２４人と求まるわけです！

 

それでは、実際の入試問題にチャレンジしてみましょうか。

 

（入試問題　Ｈ２８年度　慶應義塾普通部中学校　大問２）

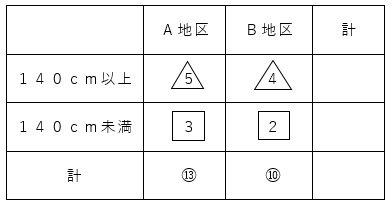
Ａ地区とＢ地区の小学生の身長について人数を調べました。Ａ地区とＢ地区の小学生全体の人数の比は１３：１０で、１４０ｃｍ以上の人数の比は５：４、１４０ｃｍ未満の人数の比は３：２です。Ａ地区の１４０ｃｍ以上の小学生とＡ地区の１４０ｃｍ未満の小学生の人数の比を求めなさい。

 

今回も、まずはグループ分けをしてみましょう。

Ａ地区で１４０ｃｍ以上、Ａ地区で１４０ｃｍ未満、Ｂ地区で１４０ｃｍ以上、Ｂ地区で１４０ｃｍ未満と４つのグループに出来ますから、先ほどの表を描いて整理してみます。

なお、先ほどの問題との相違点は、実際の数は与えられていませんが、かわりに比が与えられている点です。

Ａ地区とＢ地区、それぞれの合計が、縦の和であることを利用します。

どれかの比の数をそろえて消し、残りの２つの比を較べる消去算であることが分かりますね。

問題できかれているのが△の比と□の比なので、○の比をそろえることを考えましょう。

そのそろえ方とは・・・。

 

長くなってしまったので、

次回のお楽しみです！

 

ということで、そろそろまとめといたしましょう。

 

～今回のポイント～

・グループが複数に別れる問題では、どんな人達がいるのかをまず考え、整理するために表を描いて考える

 

ということでした！

本日はここまで。

それではまた次回、お会いしましょう。