みなさん、こんにちは。受験ドクターのAです。
受験ドクターで算、国、理、社の四科目を指導させていただいている幸せな講師です。
本日は理科の思考力問題について説明したいと思います。
理科についての話題をいくつか書かせていただきましたが、理科には典型的な知識問題、計算問題があります。
これらは、問題集や模試でよく出題されるので、慣れることが出来ます。
ところが、入試問題では見たことがない、現場思考が要求される問題が出題されることがあります。
以下がその典型問題になります。平成28年度浅野中学からの抜粋です。
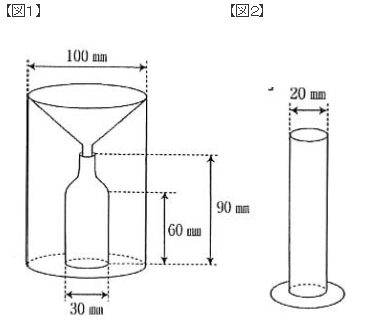
今、【図1】のような簡易雨量計を製作し、1時間の降水量を測ることにしました。
1時間後、貯水びんには深さ70mmの雨水がたまっていました。
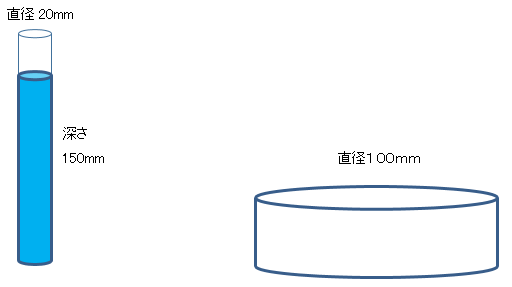
貯水びんの雨水を【図2】のような直径20mmの雨量ますに移すと、水の深さは150mmになりました。
このときの雨量は何mmですか。必要ならば、小数第1位を四捨五入して、整数で答えないさい。円周率を用いる場合は3.14としなさい
化学分野や物理分野の計算問題はよく見られる問題ですが、地学分野からの計算問題の出題は少なく、練習量も少ないはずなので、現場思考が大切になります。
さて、
天気予報は日常生活と密接しているので、毎日テレビニュースで見ている方が多いと思います。
さりげなく出てくる「午前〇時の降水量は〇〇mmです。」などもよく考えれば、いったい、何時から何時までに降った雨なのか考え込むことになります。
たとえば午前9時の降水量が10mmだとすると、これは、午前8時から午前9時までの1時間に降った雨を集めたときの高さが10mmになったということです。
ここで大切なことは、雨を集める容器です。
雨が入る入口の面積と、雨がたまる部分の底面積が同じでなければならないのです。
要するに、雨を集める容器が柱(ちゅう)でなければならないのです。
柱(ちゅう)であれば、円柱でも三角柱でも六角柱でも何でも構いません。
そこに1時間でたまった水の高さが、降水量と呼ばれるものの正体です。
よく考えてみると、プールに1時間に貯まる雨の高さと、円柱状のコップに貯まる雨の高さは同じであることが分かると思います。
それでは、本題に戻って問題を解いてみましょう。
先ほどの説明から、【図1】の簡易雨量計に書かれている、底面の直径30mmだとか、高さ60mm、90mmだとかは、この問題で必要でしょうか?
そうです!
全く必要がないのです。
さらには、文章中に書かれている「70mmの雨水がたまっていた」も問題を解くうえで全く必要ありません。
雨が入る面積だけは必要なので、雨の入り口の面積を求めるための直径だけは必要です。
難しく感じた生徒もいたかと思いますが、読解力と算数の基本で解ける問題です。
左の水を右の容器に移すだけが、この問題の答えになります。
先ほども申し上げましたが、問題や図には色々な数字が書いてありますが、一切関係ありません。
直径の比が20:100=1:5なので底面積の比が1×1:5×5=1:25になります。
よって、深さの比は25:1となり、右の容器には6mmの深さまで水が入ります。
底面積を1と考えて、左の水量は1×150=150
右の深さは150÷25(右の容器の底面積)=6mmとしてもいいかもしれません。
<まとめ>
理科の思考力問題に出会ったら、まずは落ち着く。
誰もが自分と同じ状況だと思う。
そして、問題をよく読む。
理解できたら、他の受験と圧倒的に差がつくが、解けなくても差がつかない。
ぜひ、受験、模試に役立ててください!