大木快です!
暑さが一向に衰えませんが、「暦の上では」もう秋。8月7日は立秋でした。
なんで暑いのに秋?…これは私自身が抱いた疑問です。
立秋は二十四節気の一つ。では二十四節気とは…古代中国に端を発しています。冬至、立春、夏至、立秋はいずれも太陽の動きを観測すればわかるのですが、二十四節気はこの太陽の動きに基づいた区分なので、暑い=夏、寒い=冬、という概念とは一切無関係。ですので、立秋を過ぎたからと言って暦の通り涼しく…なるはずがない!!
さて今回は、前回大好評を博した図形問題の裏ワザを引き続き紹介します。
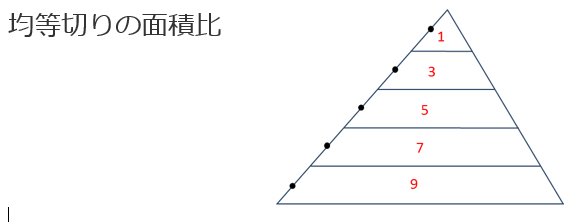
まず前回の均等切りの面積比のおさらいです。
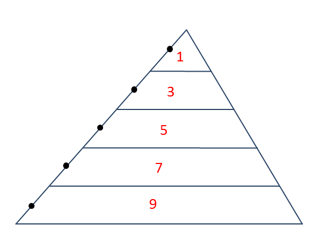
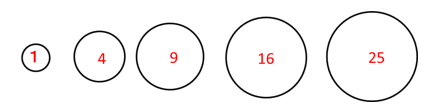
三角形を均等な幅に刻むと、面積は1,3,5,7…とあらわすことができる。
均等でない分割も、均等に刻み直すことで、均等切りの形に持ち込むことができる。
今回の材料はこの「均等切り」。
これをちょっとアレンジして、立体図形の回転体の問題に活用していきます。
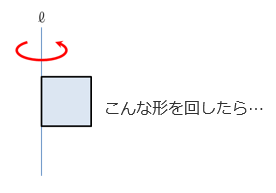
まず回転体の確認から。
円柱ができました。体積は、底面積×高さですから、
1×1×3.14×1=3.14cm3
で
は最初の問題です。まずは軽く桜蔭中(H28より抜粋)から。
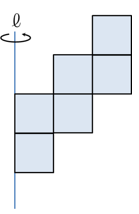
問題1
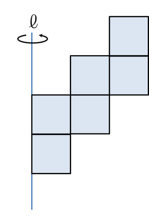
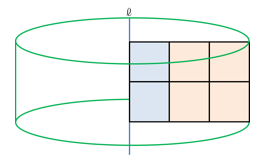
図のように1辺=1cmの正方形を配置し、直線ℓの周りを1回転してできる立体の体積を求めよ。
内側から順に、円柱、筒型、筒型の3個が組み合わさった立体ができていそうですね。
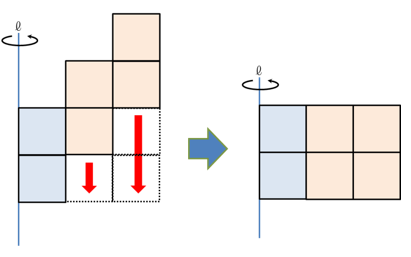
ここで、その3つの立体をずらすと…
はい、1つの大きな円柱ができました。
体積は3×3×3.14×2=56.52cm3ですね。
えっ?これのどこが裏ワザかって…そうなんです。
ここからが裏ワザです。
まず、均等切りの面積比を少々アレンジします。
まずはこの問題。
問題2
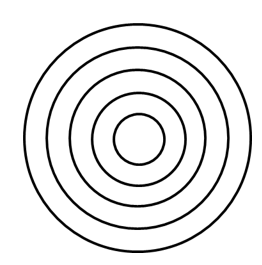
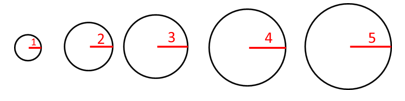
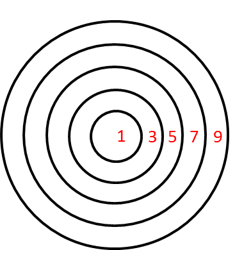
半径が1,2,3,4,5の円を組み合わせてのような図を作りました。これをダーツ型と呼ぶことにします。
このダーツ型において、区切られた5つの部分の面積比を内側から順に答えなさい。
まず
5つの円は相似な図形ですから、三角形のときと同様に考えて
五つの円の面積比は、
1×1:2×2:3×3:4×4:5×5
=1:4:9:16:25
となります。これを用いて、
円で仕切られた図形の面積比は、先ほどの1:4:9:16:25の隣同士の差を取って、内側から順に、
1:3:5:7:9…
やっぱり奇数が来た。
そして、次の問題。
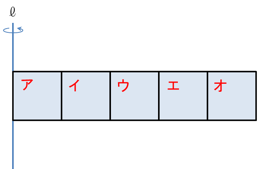
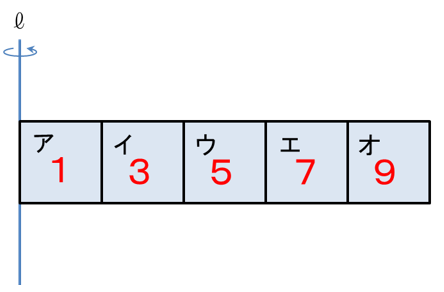
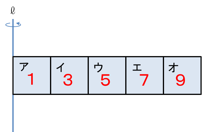
問題3
正方形5枚を組み合わせた図のような図形を、1回転して得られる立体のうち、ア、イ、ウ、エ、オが通過する部分の体積比を求めなさい。
5つの部分は高さが等しいですね。ということは、
ア、イ、ウ、エ、オを回してできる立体の底面積を比べればよいわけです。
あれっ?さっきのダーツ型がア、イ、ウ、エ、オの底面になっているではないか。だとすると、体積比はもしかして…
やっぱり奇数が来る。
これを用いて
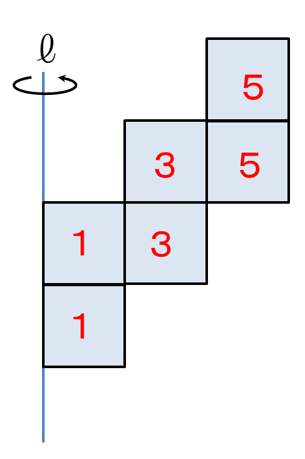
先ほど華麗に?解いた問題1を料理すると、
①内側から順に1,3,5…の奇数を書き込む
こうなります。
②数字の合計を求める。はい、18です。
1にあたる体積が一番初めに求めた3.14cm3でしたから、求める体積は円柱の18個分、すなわち
3.14×18
ということになります。
ということは、内側から順に1,3,5…の数字を書いて合計すれば、それ以外のことは何も考えなくて…
いいんです。
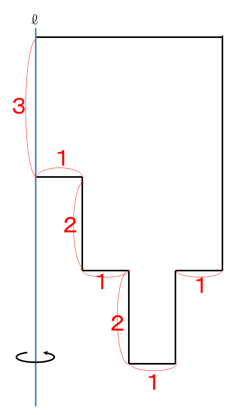
こんな問題もありますよ。東洋英和(H24・A日程)の問題です。
左のような図形を1回転してできる立体の体積を求めなさい。
下に飛び出した部分を、引っ込んだ部分に移し替えると…1つの円柱に、
なってませんからね。
危ない、危ない。軸からの距離が違うので、同じ立体になりません。出題者の仕込んだ罠に引っかかるところでした。
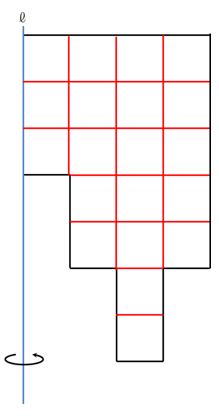
でも、私たちにとっては、そんなひっかけなどどこ吹く風。ひとたび裏ワザを手にしてしまったが最後、いやでもこんな風に見えてしまいます。
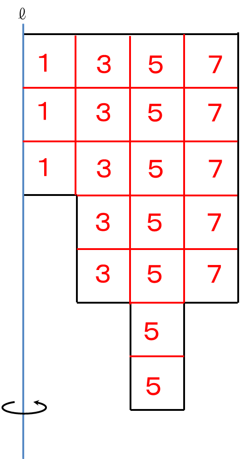
・正方形のマス目に分割
・内側から順に1,3,5,7を書き込む。
手が勝手動いて1,3,5…と数字が埋まり、合計=88が出て、
88×3.14で答えが「自動的に」出てしまう。
なぜ引っかからないか?それは、
何も考えてないからです。
今回も裏ワザの醍醐味、味わっていただけましたでしょうか。
回転体の問題は、実際にどんな立体になるかをしっかり考える力を見る材料として頻出です。(ここではその裏をかいくぐってしまいました)
しかも、体積のみ求めさせるケースが結構多いので、回転体の問題が出てきたら、「体積だけ」であることを願いましょう。体積だけなら、この裏ワザで瞬殺して、かなりの時間短縮につながるでしょう。
ではまとめです。
ダーツ型分割
正方形を組み合わせた図形の回転体の体積を求める問題において、
・内側から順に1枚当たりの体積は1,3,5,7…となる。
・分割されていないときは、自分で分割する。
・どんな立体になっているか考える必要はない。
※使用上の注意
体積を求める問題に有効。表面積を聞かれたら、正攻法でお願いします。
それでは、また。