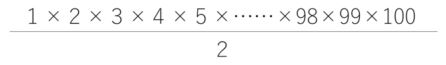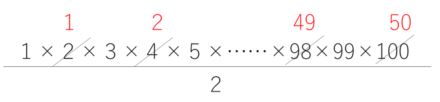みなさん、こんにちは。受験ドクターの亀井章三です。

５月です。連休も終わり、夏休みまで祝日がありません。
ゆっくりはできませんが、じっくり勉強にとりくむには最適な時期です。

今日は、わかる人にはわかる、でも理解するまで大変という問題の解法を
ご紹介いたします。

問題　下のように１から１００までをかけた数をAとします。
　　　　１×２×３×４×５×……×９８×９９×１００＝A
　　　　このAについて次の問いに答えなさい。
(1)Aを２で割り続けると何回割り切ることができますか。ただし、割り切れるとは商が整数になり余りが出ないことを指します。
(2)Aを６で割り続けると何回目で割り切れなくなりますか。

この問題のポイントは、「割り算を分数に置き換える」「割り切れる＝約分して分母が
１になる」という２つです。

まず割り算を分数に置き換えるです。
６÷３は、６つのものを３つに分ける、という意味なので、６/３　と同じです。
そこで、Aを２で割る、という問題を分数に置き換えます。

そして「割り切れる＝約分して分母が１になる」ですが、割り切れるという
ことは答えが整数になるということ。整数は分母が１の分数と考えられま
すので、約分して分母が１になれば割り切れたと考えられます。

この分数が２で何回約分できるかを考えるのが、（１）の問題です。
1から100まで100個の数がありますが、2を約分できるのは2の倍数だけです。
そうすると、１から100の中に2の倍数は100÷2＝50個ありますので、まずは
50回割り切ることができます。

もう2の倍数は残っていませんが、2の倍数を2で割った答えに注目します。

そうすると、割った答え1～50の中にまだ2の倍数があることに気づけます。
この中にある25個の2の倍数で、さらに約分（割り切る）ができます。

このようにして割り算を繰り返すだけで、何回割り切れるかを求めることができます。
ただし、この方法は「割る数が素数（１とその数でしか割り切れない数）」のときだけ
使うことができます。「3で何回割り切れますか」や「5で何回割り切れますか」は
大丈夫ですが、「6で何回割り切れますか」や「20で何回割り切れますか」は使え
ません。

では（２）6で割り切れなくなるのは何回目？を考えましょう。

重要なのは「6を割り切るのは6の倍数だけではない」ことです。
それは2の倍数と3の倍数があれば、力を合わせて約分できる！という
ことです。
ですから、6の倍数の個数を数えるのでは正しい答えが出せないわけです。

ということで「2で割り切れる回数」と「3で割り切れる回数」の両方を調べて…
となりますが、ちょっと待ってください。
両方調べるのは面倒ですよね。このブログのように（１）で「2で割り切れる回数」
を求めているのであれば、まだ大変ではないのですが。

そんなときは、お寿司で考えます。

お寿司の握りは、シャリ（ごはん）」と「ネタ（魚）」から出来ています。
ここにシャリが５つと、ネタが３つあります。お寿司はいくつ出来ますか？
そう、お寿司は３つしかできません。つまり、いっしょにする場合は少ない
ほうに合わせることになるわけです。

この考えを（２）に使いましょう。
「2で割り切れる回数」と「3で割り切れる回数」は3のほうが少ないことは
わかります。
つまり、この問題は
Aを３で割り続けると何回目で割り切れなくなりますか。
と同じになるわけです。この問題の置き換えこそがポイントです。

あとは（１）と同じように割り算を繰り返します。
100÷3＝33あまり1
33÷3＝11
11÷3＝3あまり2
3÷3＝1
33＋11＋3＋1＝48　　よって3で48回割り切ることができます。

最後にもう一つ間違えやすい箇所があります。問題は「割り切れなくなるの
は何回目」ですから、48に1を加えて49回目と答えないといけません。
算数は最後の最後まで油断しないで取り組みましょう。

今回は初級編として「素数で割り続ける」ときと、「２つの素数の積で割り続
ける」ときをご説明いたしました。
次回は中級編として「0が並ぶ個数」と「9で割り続けるとき」をご説明いたし
ます。お楽しみに。