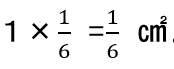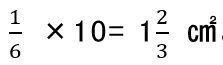みなさん、こんにちは！受験ドクター算数科のA.K講師です。

秋、真っ盛り。
秋と言えば…。やはり、紅葉ですよね！
関東地方はまだまだですが、もう半月くらいたつと街中の葉が緑、黄、紅と様々に色づいてくるはず。
毎年、この時期になるとそのコントラストに感動し、
「四季のきれいな日本に生まれて良かったなぁ。」
と感慨に耽る私なんです。
特に、旅行好きのA.K講師からすれば京都の嵐山・渡月橋（A.K講師は音楽好きなので、今年リリースされた同名の某歌手の曲をよく聴いて口ずさんでおります…。）は本当に美しいです。一瞬、我を忘れてしまうレベルです。ぜひ、皆様もお時間があれば訪れてみてくださいね！

…前置きが、いつも以上に長くなってしまいましたm(_ _)m
気を取り直して、今回のテーマは…。

あれっ？
前回と同じじゃん。。

そう、続きです。
前にお伝えした対称軸と面積比の考え方を基にして、入試問題にチャレンジしてみましょう！！

【問題】平成２９年度　早稲田中学校　第１回入試　大問２（２）より（一部改訂）
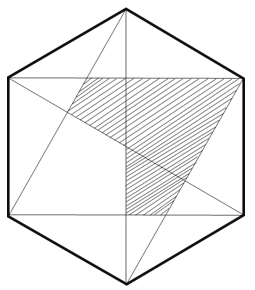
下図の正六角形の面積は6㎠です。斜線部分の面積は何㎠ですか。

こんな変な形の面積、一見すると求めるのが不可能に見えますよね。
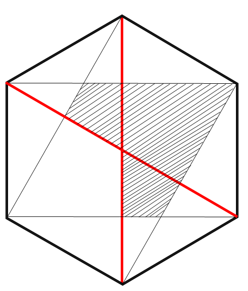
ですが、前回お伝えした対称軸が何本か引いてあることに注目してみましょう！

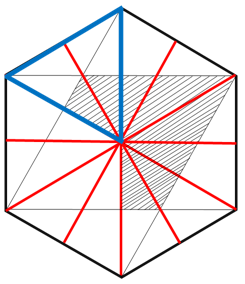
残りの線も、全て引いてみましょう！
そして、左上の青い正三角形に着目してみてください…。

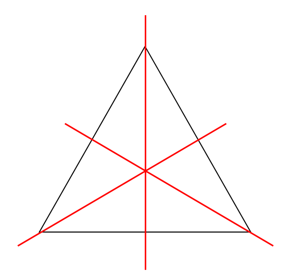
向きを変えると…

前回お伝えした内容と全く同じ話になりました！！

正三角形の面積は全体の1/6 ですから、

そして、正三角形の1箇所分はさらにそれを6等分しているので、

左上と右下の部分については、斜線部分はそれぞれ2か所ずつあるので計4か所。
右上と右側の部分については、斜線部分はそれぞれ3か所ずつあるので計6か所。

よって、全部あわせると10か所分あるので、

となるわけです！

以前にお伝えしたかもしれませんが、入試問題は一見難しそうに見えても、一つ一つ解きほぐしていけば、その全てが基本となる知識で出来ています。
私たちは、その知識や理屈を少しでも多く、皆様に分かりやすくお伝えできればと思っております！

本日の内容、いかがでしたか？この辺で今日のまとめとしましょう。

～本日のまとめ～

①正六角形は各頂点を通る対称軸を引いた場合、6つの面積の等しい正三角形にわかれる。
②正三角形は線対称な図形であり、3本の対称軸を引くと6つの面積の等しい三角形にわかれる。

では今日はここまで。
今回も長々とお付き合いいただき、ありがとうございました。
次回は…入試に打ち勝つためには、やはり避けては通れない「割合」についてスポットライトを当てていく予定です。

それでは。次回も、お楽しみに！！