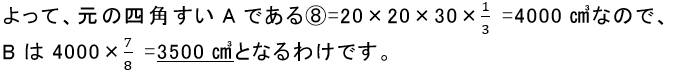みなさん、こんにちは!受験ドクター算数科のA.K講師です。
7月ももう半ば。
皆さんは、夏はお好きですか??
私は、実をいうとキライです(><)A.K講師は冬生まれなので、あっつい夏は苦手なのです…溶けてアイスになってしまいそうです汗
こんなに暑い日が続いてしまうと、海に飛び込みたくなりますね^^;
特に、外で長時間の運動をするお子様は、こまめな水分補給を怠らないようにお気をつけくださいね。
それでは、今日の本題へ…。
前回、水量グラフと立体図形の融合単元として、以下の自作問題を出させていただきました。憶えていらっしゃるでしょうか。
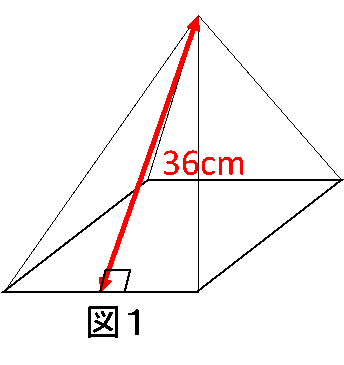
図1のような四角すいA(底面は1辺が20cmの正方形で、高さは30cm)があり、Aの高さの半分の所で、底面と平行な面でAを切断しました。
切断して2つにわかれたうちの大きい方の立体をBとします。Bを2つ用意し、切断面同士をつなぎ合わせて立体Cをさらに作り、向きをそのままにしてCを直方体の形をした空の水そうの中に置きます。
ここで、水そう内に1秒あたり50㎤の割合で水を入れていくと、水を入れ始めてからの時間と水そう内の水の深さの関係は以下の図2のようになりました。
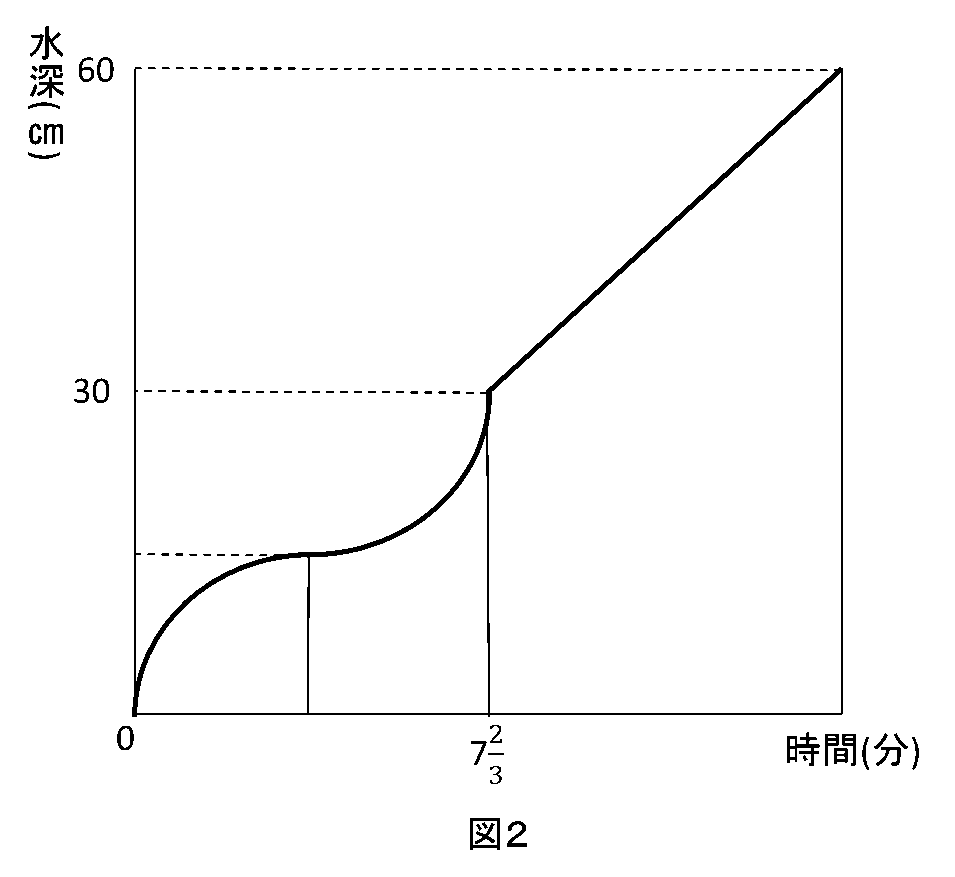
(1)立体Bの体積と表面積を求めなさい。
(2)この水そうの底面積を求めなさい。
(3)この水そうは何分間で満水になりますか。
それでは、今回はポイントを交えつつ各問を解題していきましょう!
(1)まず、もとの立体Aである四角すいを問題文の指示にしたがって切断すると、以下のようになります。
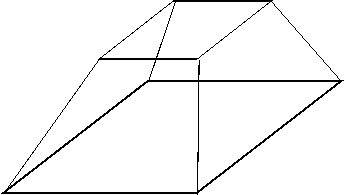
立体Bは、大きい方の立体ですから以下の形になります。四角すい台と呼ばれるものです(底面がどちらも正方形となります)。
ここで、切り離した四角すいと、もとの四角すいの体積の比を考えてみましょう。
もとの高さの半分で切ったので、各々の高さ比は1:2です。形は同じで、大きさが違う立体同士なので相似ということになります。
相似の場合。平面図形で長さ比が1:2のときは、面積比が1×1:2×2=1:4となります。これは、面積を出すときには縦×横、あるいは底辺×高さといったように長さを2回かけあわせるからです。
では、立体の場合はどうなるでしょうか?長さを3回かけあわせるので(縦×横×高さ)、長さ比が1:2の場合は体積比が1×1×1:2×2×2=1:8となります!切り離した四角すいを①とおくと、立体Bは⑧-①=⑦です。

次に、表面積です。底面のうち、大きい正方形は20cm×20cm=400㎠で、小さい正方形は10cm×10cm=100㎠です。立体Aの側面積(以下の図の△ADE)は20cm×36cm÷2=360㎠となり、以下の図の台形BDECが求めるべき側面積となります。
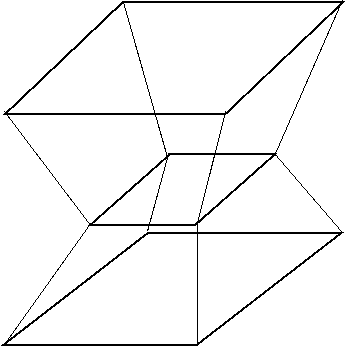
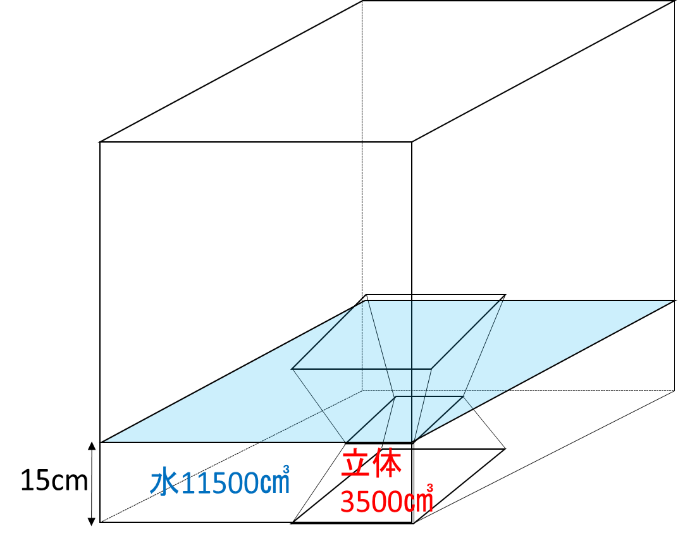
(2)Bを2つ重ねた立体Cは、以下の形です。
よって、上図から容器の底面積は(11500+3500)÷15=1000㎠となります。
いかがでしたでしょうか。なかなか、骨のある問題で苦労した人もいたのではないでしょうか!?
それでは…この辺で今回のまとめといたしましょう。
~今回のポイント~
・相似の図形同士であれば、長さを2回かけたものが面積であり、3回かけたものが体積である。比にも応用できる。
ということでした。
では今日はここまで。
次回は、皆さんに名探偵になってもらう(!?)予定でいます。
もうすぐ、ドクターでは7月24日から夏の暑さに負けないような、最高にホットな夏期講習がスタートしますよ!
一緒に、この夏を頑張って最後まで走り抜けましょうね。
では、またお会いしましょう!