みなさん、こんにちは!受験ドクター算数科のA.K講師です。
6月ももう半ば、梅雨の季節がやってきましたね。ジメジメして、洗濯物もなかなか乾かない季節ではあるけれど、雨の多く降るこの時期も日本の四季の一つとして私は好きです。傘を常に持っていないといけないのが、少々面倒ですが^^;
それでは、今日の本題へ…。
先ほど、少しだけ梅雨の話をしました。梅雨⇒雨⇒水⇒水量グラフということで、(ものすごく強引ではありますが汗)
お待たせしました、今回は私が作った問題を考えてみてください!
タイトルにもありますが、水量グラフ・立体切断の2つのテーマを絡めた問題を作成してみました。なかなか難しいですが、途中でヒントも出すのでぜひ最後まであきらめないで挑戦してみてください。
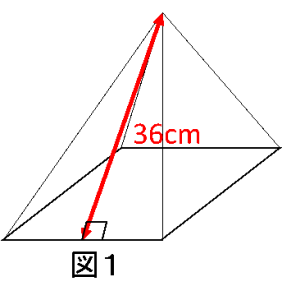
(問題)図1のような四角すいA(底面は1辺が20cmの正方形で、高さは30cm)があり、Aの高さの半分の所で、底面と平行な面でAを切断しました。
切断して2つにわかれたうちの大きい方の立体をBとします。Bを2つ用意し、切断面同士をつなぎ合わせて立体Cをさらに作り、向きをそのままにしてCを直方体の形をした空の水そうの中に置きます。
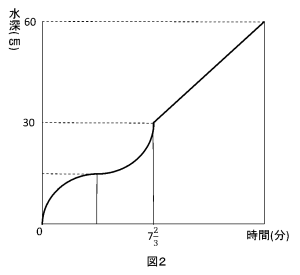
ここで、水そう内に1秒あたり50㎤の割合で水を入れていくと、水を入れ始めてからの時間と水そう内の水の深さの関係は以下の図2のようになりました。
(1)立体Bの体積と表面積を求めなさい。
(2)この水そうの底面積を求めなさい。
(3)この水そうは何分間で満水になりますか。
渾身の一題です。「ムムム…。」と頭を悩ませる人も多いことでしょう。どこから取り掛かればいいのか、と考え込んでしまうかもしれません。
そんな皆様のために、ヒントを出しましょう。
(1)については、立体Bの形状がどのようになるのか、しっかりと考えなければいけません。そのためには、まずは元の四角すいを自分の手で描き、問題文の指示に従って手を動かして作業をした上、Bの形を暴いていきましょう!
(2)については、(1)よりBの形が分かれば、水そうにCをどのように入れたのかもわかります。
そこで、図2のグラフに注目。「なぜ?」グラフの前半部分が、扇形の弧のような形になっているのか。それは立体Cの形が…おっと、これ以上は言えませんね。賢い皆様の頭で考えてみてください!
ここまでで考えてきたことと、1秒あたりに入る水量、そしてグラフに水が入りきる時間も与えられているので答えが求まるはず。
(3)については、底面積が分かれば水そう全体の容積も分かるので、満水になる時間も分かります。
今回も様々なことをお伝えいたしました。
では、ここで本日のまとめといたしましょう。…とは言っても、今回出題した問題を解くためのヒントみたいなものになってしまいますが。
~今回のポイント~
・水量グラフの問題では、グラフの形と変化のある部分に着目し、「何が」起こっているのかを考える癖をつける!
・1分あたりに入る水の体積×時間(分)=水の体積 になる!
ということでした。
では今日はここまで。
次回は、後篇として考え方のポイントを交えて今回の問題を解説していきます!!それまで、じっくりと落ち着いて、答えを出すことに専念してくださいね。
それではまた次回、お会いしましょう!