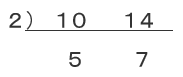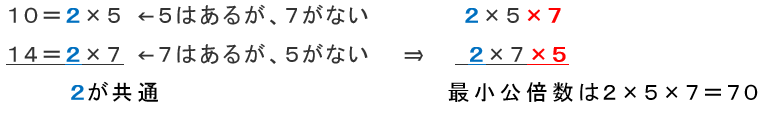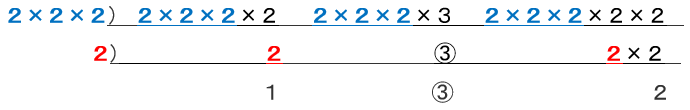みなさん、こんにちは！受験ドクター算数科のA.K講師です。

 

梅雨もあけ、本格的な夏がやってきましたね！

みなさんは、夏と言ったら何を思い浮かべますか？

花火、お祭り、海、スイカわり、かき氷、アイス……すみません、食べ物ばかりになってしまいました^^;

 

でも、みなさんが忘れようとしたくてもどうしても忘れられないものがありますね？

そう、それは…

学校の宿題！！

 

夏休みが始まったばかりですが、

「後でやるから大丈夫、大丈夫！！」

って思っているそこのアナタ…その考え方は危険ですよ？

 

例えば、大人の世界だと仕事では納期が決まっているものです。

「この仕事はこれくらいの分量があるから、締め切りの３日前には手を付け始めなきゃ…。」

と先のことを考え、スケジューリングをします。

 

君たちは大丈夫かな？？

「僕は子どもだから！！」

という気持ちじゃダメですよ。

宿題の分量を考えずに、夏休みの最後の日に全部やればいいや…と思っていると、

「あれもやってない！これもやってない！！こんなの物理的に無理だよー」

となってしまいかねませんね。

休みを満喫するのも大事だけれど、きちんと勉強の計画を立てるのも大事ですね。

 

さて、今回は算数を面白いと思ってもらえるような話をしていきたいと思います。

お題は、数の性質で何かとお世話になる「最小公倍数」。

 

みなさんは、塾で逆さ割り算（あるいは連除法）を習いましたよね？

 

①１０と１４の最小公倍数を求めなさい。

このＬ字型の数字をすべてかけあわせ、

２×５×７＝７０　と求めることが出来ます。

 

なぜ？なぜこの方法で求めることが出来るのでしょうか？？

それにはちゃーんと、理由があるのです。

 

ここで頼りになるのが素因数分解（数を素数の掛け算の形であらわすこと）です。

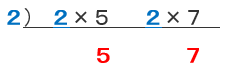
素因数分解をした形で、先ほどの逆さ割り算を見てみましょう。

ちょっと分かりづらいので、こうしてみましょう。

となるわけです！つまり、足りない数を補っていたというわけですね。

ただ、それぞれの数でいちいち素因数分解をしていると時間がなくなってしまうので、

それを省略して答えを求めるのに特化したのが逆さ割り算なのです。

 

「２つの数だと問題ないけど、３つの数で出来ない時があるんだけど！」

「なんで３つの場合は、先に割れる数で割ってから２つで割れる数を考えなきゃいけないの？」

っていうそこのキミ。

大丈夫です。連除法は君を裏切りません。

 

というわけで…２問目に行ってみましょう！！

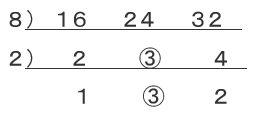
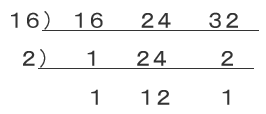
②１６と２４と３２の最小公倍数を求めなさい。

○の数字は割れないので、そのまま下に降ろします。

このＬ字型の数字をすべてかけあわせ、

８×２×１×３×２＝９６　と求めることが出来ます。

 

なぜ？なぜ３つの場合だと、○の数字のように割れない数があってもいいのでしょうか？

それにはちゃーーんと、理由があるのです。

 

ここで再び、素因数分解の出番です。

あらためて先ほどの逆さ割り算を見てみましょう。

 

分かりづらいので、先ほどと同じように補うべき数を見てみましょう。

 

となるわけです！！

逆さ割り算の２段目で、３を放っておいて残りの数を２で割ることにも納得がいきましたね。

２を１６と３２から消すことで、２４の３と３２の２を残すようにしたかったからです。

 

ちなみに、、、

Ｌ字型の数をかけると１６×２×１×１２×１＝３８４となりますが、これは誤りですね。

なぜ先ほどの９６と違う答えが出たのか、そして何故いきなり１６で割ってしまってはいけないのか…。

 

それはみなさんの頭で考えてみてくださいね。「１６で割ったら、足りない数の補い方がどう変化するのか？」という点に着目したら、きっと分かるはずです！

全てを教えちゃうと、自分の手で考える力が育たないので、みなさんにお任せします。

君たちなら出来る！！

 

…ということで、本日のまとめ。

 

・最小公倍数の求め方の理論は、素因数分解から成り立っている。

・上記の理論を簡略化したものが逆さ割り算を使った連除法である。

塾によっては、最小公倍数の求め方を教えないこともあったりするので、これを機にしっかりと覚えておいてくださいね。

 

次回は引き続き、算数のなぜなぜ？を解明していこうと思いますので、乞うご期待。

今回はこの辺で失礼いたします。

それではまた、近いうちにお会いしましょう。