皆さま、こんにちは！

さて、前回はつるかめ算の基本をおさえていれば、それだけで入試問題も十分に解けることを解説しました。
ポイントは以下の２点でした。
①その問題がつるかめ算だということがわかるか
②つるかめ算だとわかったときに、どのような処理をするか
ポイントさえ押さえていれば、特別な知識やテクニックがなくてもちょっとした応用問題なら対応できます。
応用問題を考える際の大切な心構えは、「どうしたら自分の知っている形に持ち込めるか？」と考えることです。
今回はそういった考え方の大切さが学べる「三段つるかめ」について考えてみましょう。

 

【普通のつるかめ算と「三段つるかめ」の違い】
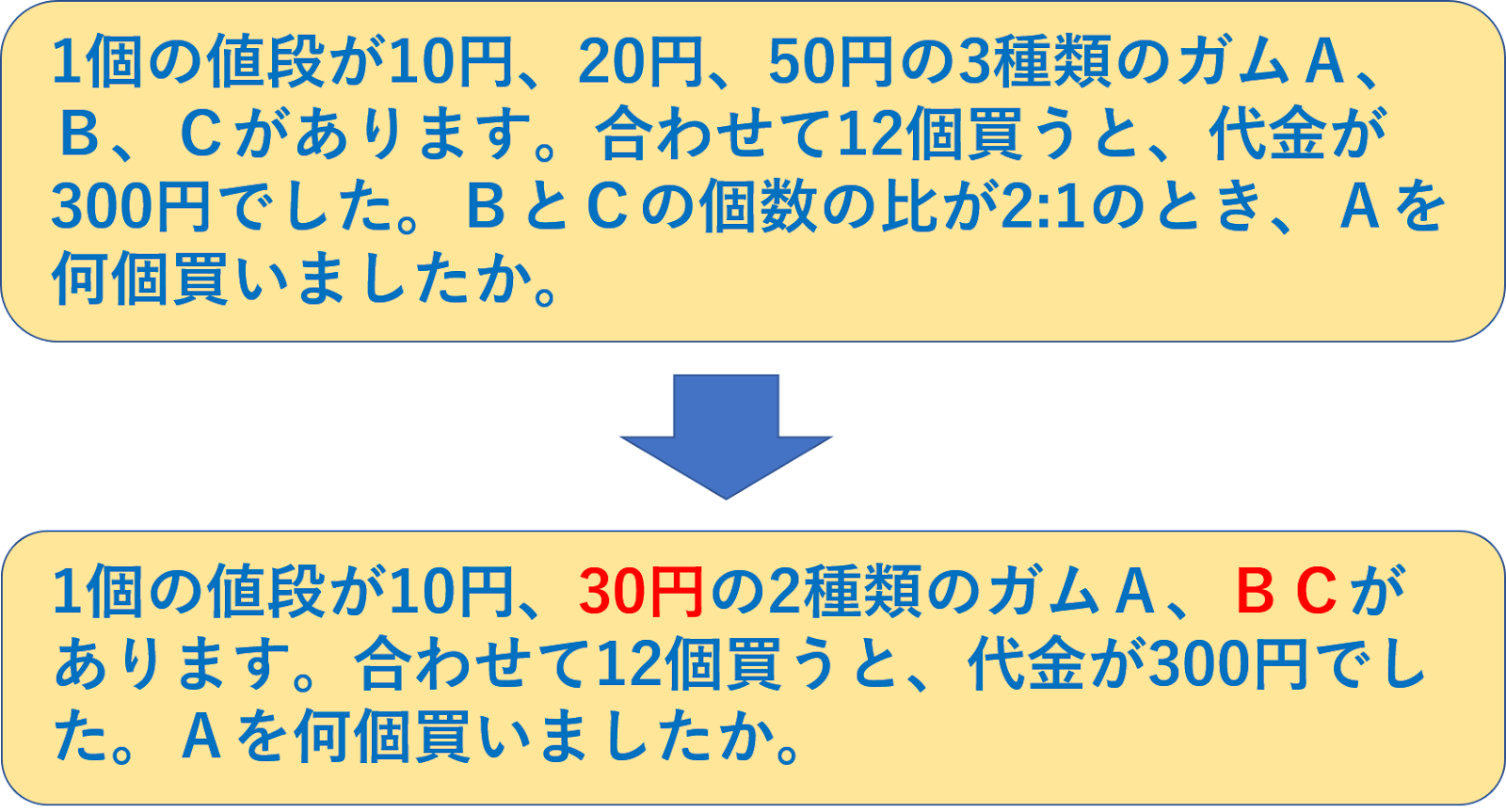
まずは以下の問題を見てください。

 

 

これが「三段つるかめ」の典型問題です。
普通のつるかめ算と何がちがうでしょうか？
まず、２種類の合計が出てきている、という点では普通のつるかめ算と一緒ですね。
買ったガムの個数の合計と、代金の合計の２つです。
２種類の合計が出てきているので、これはつるかめ算です。
一方で、普通のつるかめ算と異なる点は、ガムＡ、ガムＢ、ガムＣと３つのものが出てきている点ですね。
今までのつるかめ算なら、つるとかめとか、りんごとみかんとか、２つのものの話でした。
それが３つのものになっているという点が、「三段つるかめ」と呼ばれる理由ですね。

 

では、このような「三段つるかめ」はどのように解いたらよいでしょうか？
先ほども書いたように、「どうしたら自分の知っている形に持ち込めるか？」と考えることが大切です。
今回の場合は、どうしたらいつものつるかめ算にできるか？と考えます。
３つのものがあるわけですから、どうにかして２つのものにすることができればいいのです。
うまくひとつのものを消すことができれば、あとはいつも通りに処理すればＯＫです。

 

【加重平均を求めてひとつに合体させる】

では、どうやったらいつも通りの２つのつるかめ算にすることができるでしょうか？
いくつか方法がありますが、今回は２つのものの平均をとってひとつに合体させる方法でやってみましょう。
ガムＢが１個２０円、ガムＣが１個５０円なので、この２つの平均を考えます。
ただし、この場合は（２０＋５０）÷２ー＝３５で、１個３５円としてはいけません。
なぜかというと、ガムＢとガムＣの個数が同じではないからです。
以前にこのブログで「加重平均」という考え方を説明しました。
平均を考えるときに、その値に「重みの違い」があるときは、必ずその「重み」を計算に入れないといけません。
この問題では、ガムＢとガムＣの個数の比が２：１なので、これを考慮しないと正しい平均は求められません。
「加重平均」について詳しく知りたい方は２０２１年１２月１４日のブログを見てください。
今回は、それはわかっているものとしてこのあとの解説をします。

 

まず、ガムＢとガムＣの個数の比が２：１とわかっていますが、これを具体的な数値として考えてしまいます。
つまり、ガムＢが２個、ガムＣが１個だとすると、１個あたりの平均の値段はいくつになるか求めるということです。
ガムＢは１個２０円で２個ですから、２０×２＝４０で、その合計代金は４０円です。
一方、ガムＣは１個５０円で１個ですから、５０×１＝５０で、その合計代金は５０円です。
すると、ガムＢとガムＣの合計代金は４０＋５０＝９０で９０円になりますね。
全部で３個の合計代金が９０円なので、平均は９０÷３＝３０で、３０円ということになります。
これが何を意味するかというと、ガムＢとガムＣを合体させて１個３０円のガムＢＣを作ったということです。
すると、最初の問題は、次のような問題に置き換わったことになります。

 

 

初めてこういった解き方をするときは、「本当にこれでいいのかなー？」と感じるかもしれません。
でも、これで大丈夫です！
実際に計算して確認してみましょう。

 

【あとはいつも通りに処理する】
ここまで来れば、あとはいつも通りに処理するだけです。
面積図でも立式でも、自分の一番やりやすい自信のある方法で処理してください。
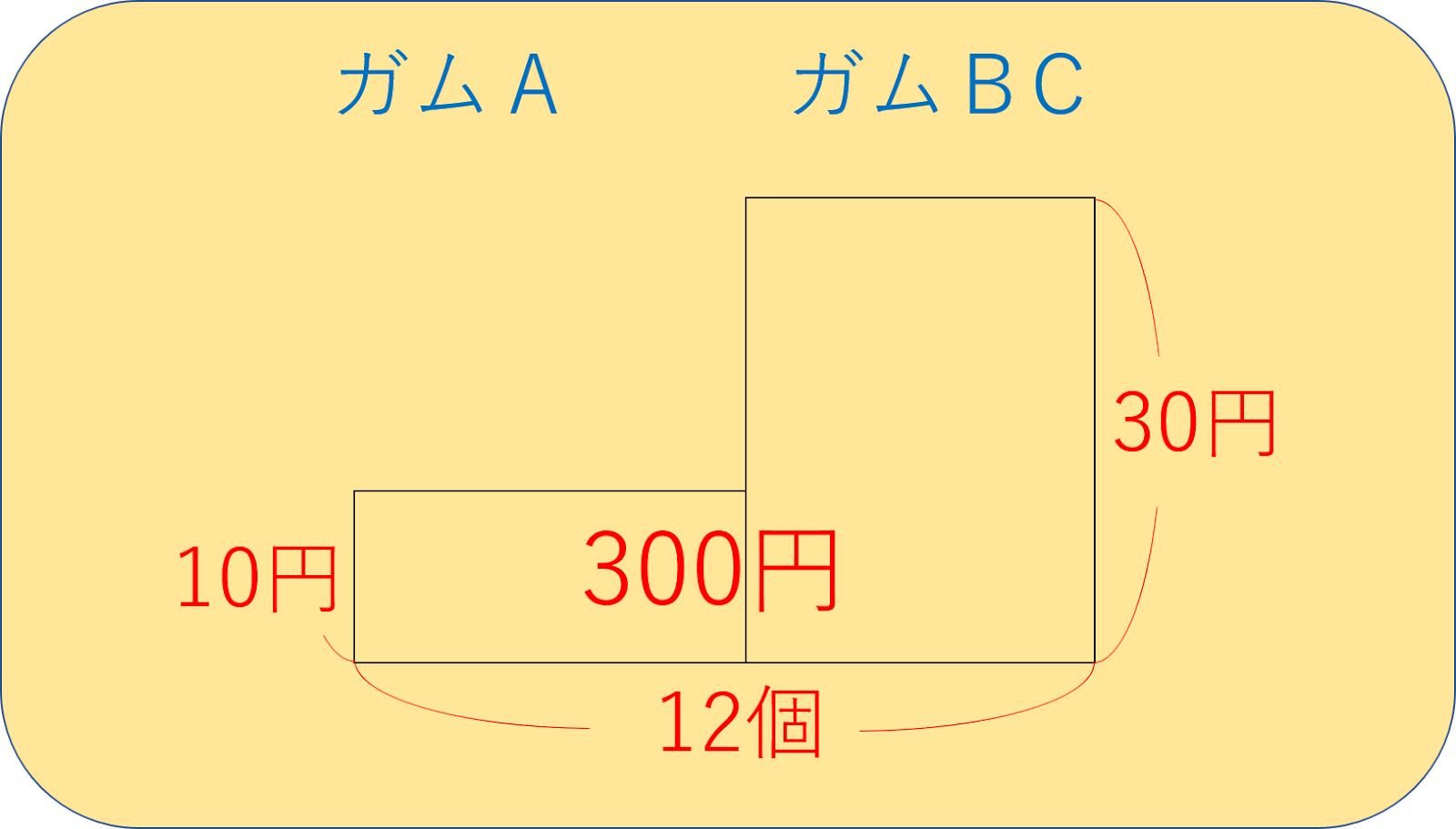
ここではいつも通り、面積図で解いてみましょう。
以下のような面積図ができますね。

 

 

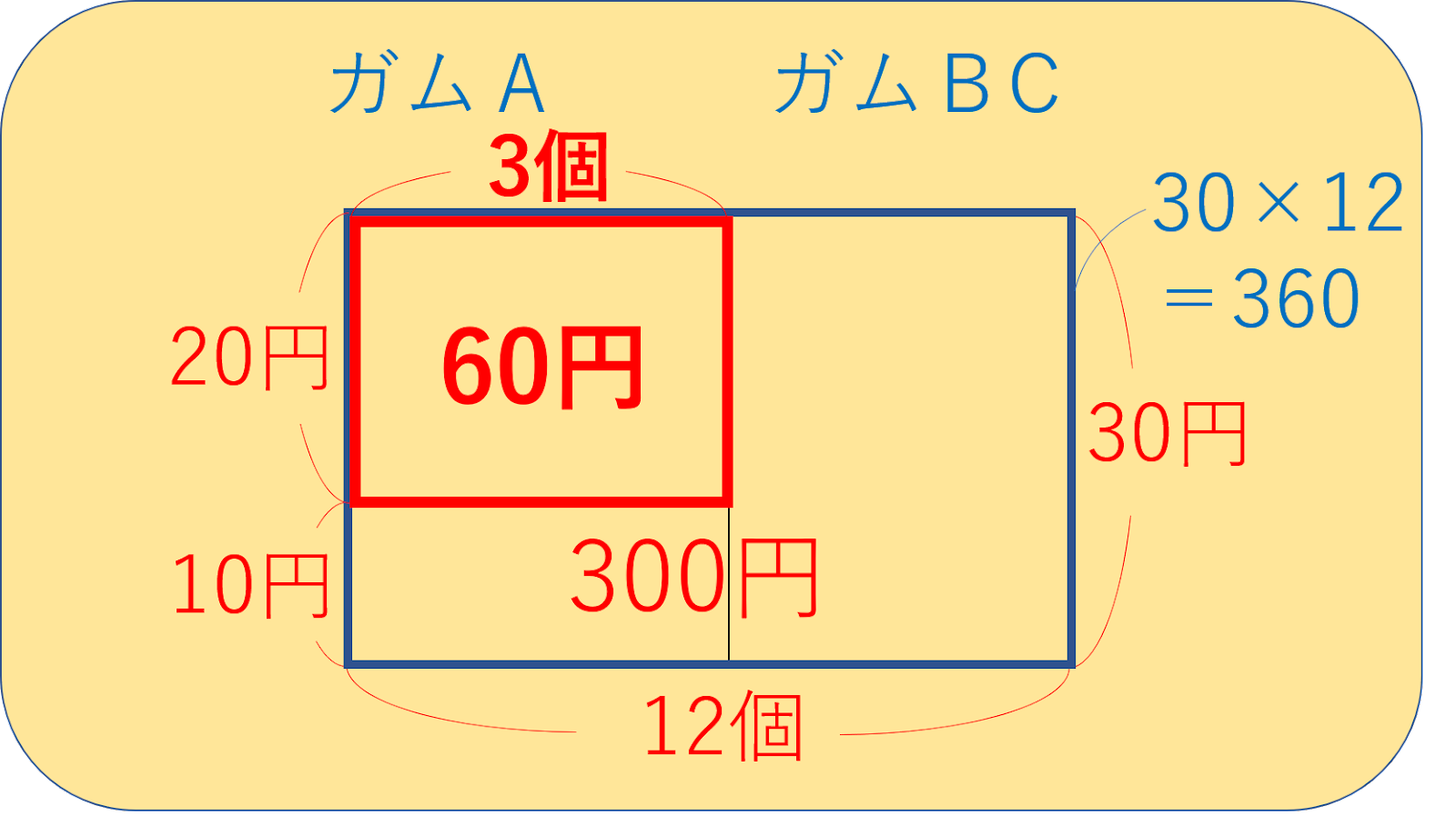
あとは左上の欠けている部分に注目すれば、ガムAの個数が求められます。

 

上図のように、いつも通りに考えればガムAの個数は３個と求められますね。
求めるものはガムAの個数ですから、答えは３個です。

 

【大切なことは確認すること】
これが正解なのですが、ちょっと待ってください！
このときに、ガムBとガムCがどうなっているのかも、念のため確認してみましょう。
まず、ガムAが３個ですから、合体させたガムBCは９個です。
でも、実際にはガムBとガムCは別のものですから、これはあわせて９個ということです。
ガムBとガムCの個数比は２：１でしたね？
ということは、９個を２：１に分ければ、それぞれの個数になるはずです。
ですから、ガムBは６個、ガムCは３個ということです。
すると、１０円のガムAが３個、２０円のガムBが６個、５０円のガムCが３個ということになりますね。
ではこれで合計金額が３００円になるでしょうか？
実際に計算してみましょう。
１０×３＋２０×６＋５０×３＝３０＋１２０＋１５０＝３００で、たしかに３００円になりましたね！
ということで、これできちんと解けているということです。
このシリーズの最初でも書いたように、大切なことは確認することです。
時間があるときは、いろいろな形で答えの正しさを確認することを心がけましょうね。

 

【今回のまとめ】
ということで、「三段つるかめ」の問題もちゃんと解くことができました。
今回のポイントは、どうしたらいつものつるかめ算にできるか？と考えることでした。
こういった考え方は様々な算数の応用問題を考える際に有効です。
前回も書きましたが、算数の応用問題は基本的な問題に新しい作業をいくつか増やすことで作られます。
どうやっていつもと違う問題に見せるかが、作問者の腕の見せ所です。
そして、そうやって作問者が巧妙に隠した問題の本質を、どう見抜くかが解く方の腕の見せ所です。
作問者との知恵比べこそが、良質な問題を解く面白さなのです。
ぜひ皆さんも、作問者の意図を見抜いて、適切な解法にたどり着けるように日々トレーニングしてみてください。

 

 

では、また次回お会いしましょう！