どうもこんにちは。
受験ドクター算数科のRS講師です。

前回はつるかめ算と面積図のお話を引き合いにしましたが、
面積図ついでに、今回から何回かに渡って「食塩水」の問題を取り上げていきます。

食塩水といえば、てんびん図（面積図）！と答えるひとも多いかもしれませんね。
食塩水の問題で面積図とてんびん図の役割は、実はまったく同じなのですが、
「食塩水？あ、てんびん図ね」なんていう乱暴な考え方をしていると、食塩水のや
り取り算などになってきたときに困る事になります。

まずはきちんと基本から学んでいきましょう。
食塩水の問題の基本的な解法は、「食塩の量の変化を追いかける」です。

次の図を見て下さい。

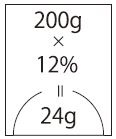
上の図は、ビーカー図というもので、上から食塩水全体の重さ、真ん中の段に濃度、
最下段のぼた餅の中に食塩の重さを書き込んだものです。
この図の書き方は、塾や先生によってもまちまちで、一番上が濃度、真ん中が食塩、
最下段が全体の重さなど、いろいろなバリエーションがありますね。多分6パター
ンあるんじゃ無いでしょうか？（笑

私は、上の図のように書いています。
これは、ちょっとしたこだわりがあって、上から順番にかけ算の式になっているの
です。
ビーカーの中にかけ算の式がある。

全体の量×濃度＝食塩の量　なので、
濃度や、全体の量が分からないときは、この式を逆算してやれば、どちらも求める
事ができますね。
まあ、これはあまり重要なポイントではなく、食塩の量／全体の量　＝　濃度
という捉え方の方がスッキリすると思う人は上下の順番は好きなように書けば良い
と思います。

〈問題〉
ビーカーAに3％の濃度の食塩水が200ｇ、ビーカーBに5％の濃度の食塩水が300
ｇあります。これらを全部混ぜ合わせると何％の濃度になりますか。

食塩水の基本は、ビーカー図です！
面積図やてんびん図じゃない。

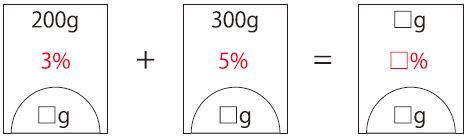
まず、問題文にあるとおりに、ビーカー図を並べて書いていきましょう。
このようになります。

では計算していきます。

食塩の量のところは、それぞれのビーカーに含まれている食塩の量なので、上からかけ算をし
ていくだけです。
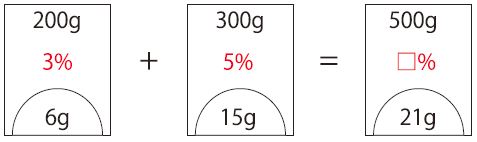
次に、これらを混ぜ合わせるので、量をそれぞれ合計していきます。

濃度のところ（％）が赤字になっている理由はわかりますか？
濃度というのは、割合のことです。
割合は、ある数量Ａとある数量Ｂを割り算して大きさを比較した数です。
ここでは、ビーカーの全体の量と食塩の量を比べた数ということですから、
3％と5％をたして8％とすることはできません。

出来上がった食塩水の濃度は、500ｇと21ｇを比べて、21÷500＝0.042＝4.2％ということ
になります。

次はどうでしょう。
〈問題〉ビーカーＡに濃度3％の食塩水が100ｇ、ビーカーＢにもある濃度の食塩水が入って
います。これらを混ぜ合わせたところ、濃度が5％の食塩水が300ｇできました。ビーカーB
の食塩水の濃度は何％でしょうか。

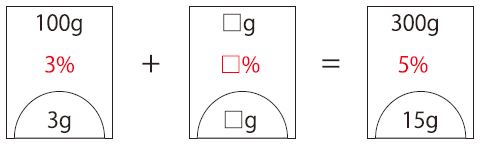
こういうことですね。

５-３＝２％　とやってはいけませんよ。
でも黒い□のところは、逆算して求められます。
どちらも、３００ー１００＝２００ｇ、１５ー３＝１２ｇと計算出来ますね。
あとは、この２数の割合を求めれば答えです。

１２÷２００＝０.０６＝６％　

さあ、では次です。
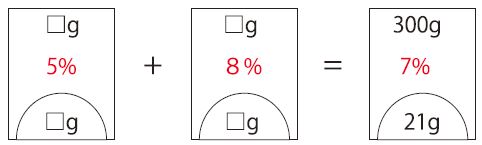
〈問題〉ビーカーAに濃度５％の食塩水が、ビーカーBに濃度８％の食塩水が入っています。
これらを混ぜたところ、濃度７％の食塩水が３００ｇできました。ビーカーAには何ｇの食塩
水がありましたか。

はい。とりあえず図にしてみましょう。

ここで困ったことに気が付くでしょうか？

逆算が出来ないのです。
全体の量を見ても、食塩の量を見ても、どちらも結果しか書かれていないので、それぞれがど
んな重さだったのか、どちらからも逆算できません。

このように、全体の量、食塩の量、どちらからも逆算の式が作れない問題の時にだけてんび
ん図が必要になるのです。

でも、なぜてんびん図ならこれが解けるのでしょう？
てんびん図とはなんぞやということも含めて基本からキッチリと説明したいと思いますので、
今回はここまで。

ではでは( ́Д｀)ﾉ～