こんにちは。算数を担当しています佐々木です。

今回は、三角形の角度・面積の問題について。
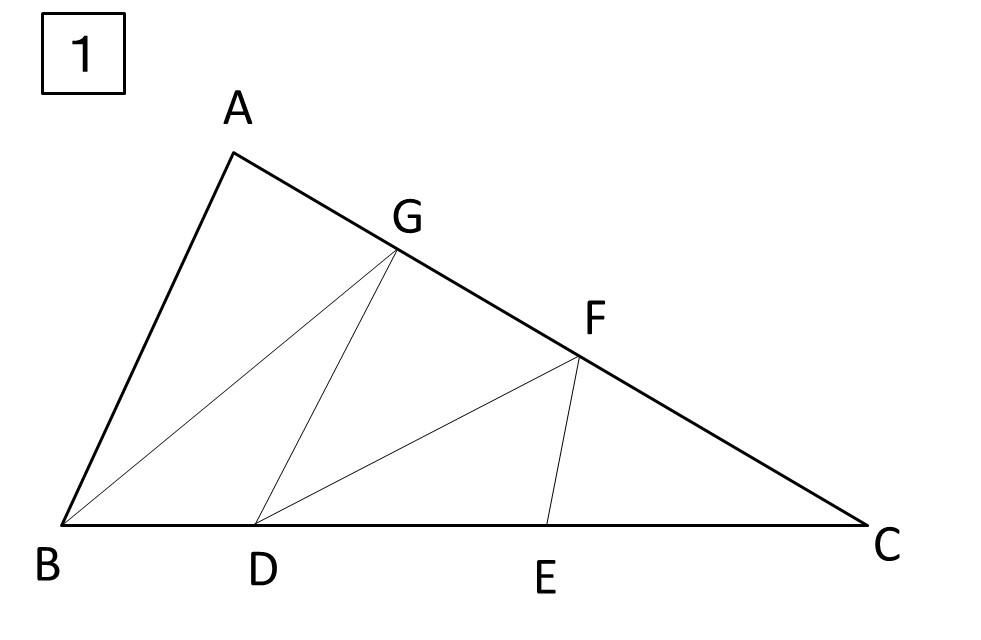
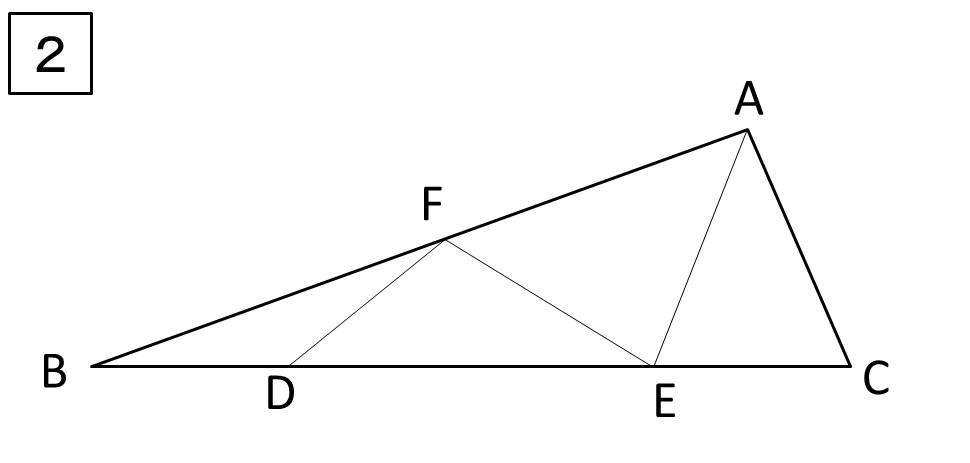
まず、下の2つの図をみてください。

 

 

すごく似ていますね。

この2つの図からどんな問題を想像しますか。
どんな問題をつくることができるでしょうか。

【1】は、辺の比や面積比を求めさせる問題でよく出てきます。
【2】は、角度を求める問題です。しかしながら、【2】の図からも辺の比を求めさせる問題をつくってもいいかもしれません。

例えば、【1】は、

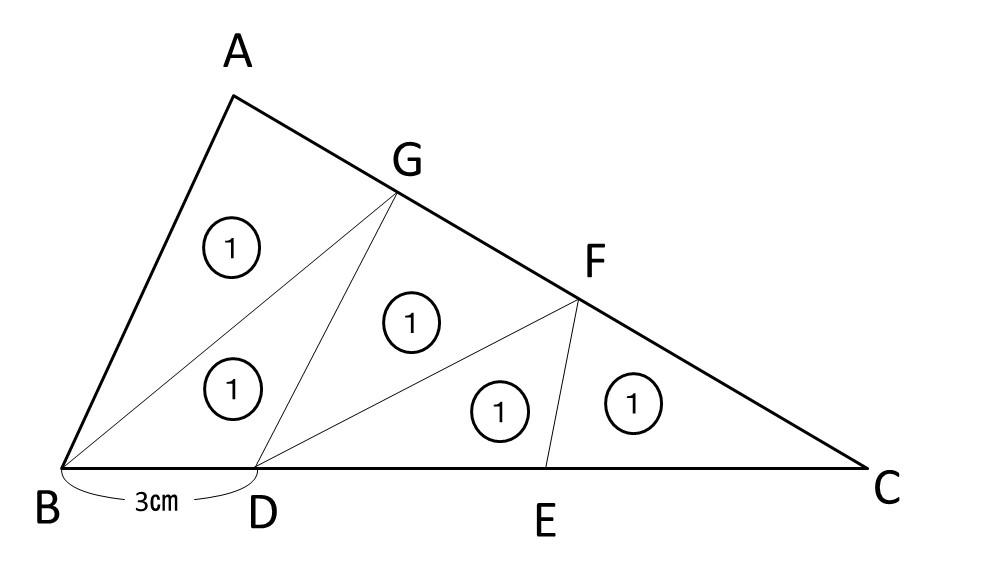
問題：三角形ＡＢＣを面積が等しい5つの三角形に分けたものです。
これについて次の問いに答えなさい。

(1)ＢＤの長さが3㎝のとき、ＥＣの長さは何㎝ですか。
(2)ＡＧ：ＧＦ：ＦＣを求めなさい。

 

(1)
解法
1 高さの等しい三角形を見つける
2 種類の比で同じ辺を表す
3 連比

この手順で解き進めていきましょう。

辺BDを使っている三角形は三角形BDG
この三角形BDGと高さが等しい三角形は、三角形GDC
頂点Gが共通である

面積比が三角形BDGと三角形GDCは、1：3のため、辺の比もBD：DC＝1：3
よって辺DC＝3×3＝9㎝

また、2つ目の高さが等しい三角形を見つけると、
今度はDEとECを比べたいので、
三角形FDEと三角形FEC　これは、頂点Fが共通

1：1のため、9÷2＝4.5㎝
答え.　辺EC＝4.5㎝

 

(2)
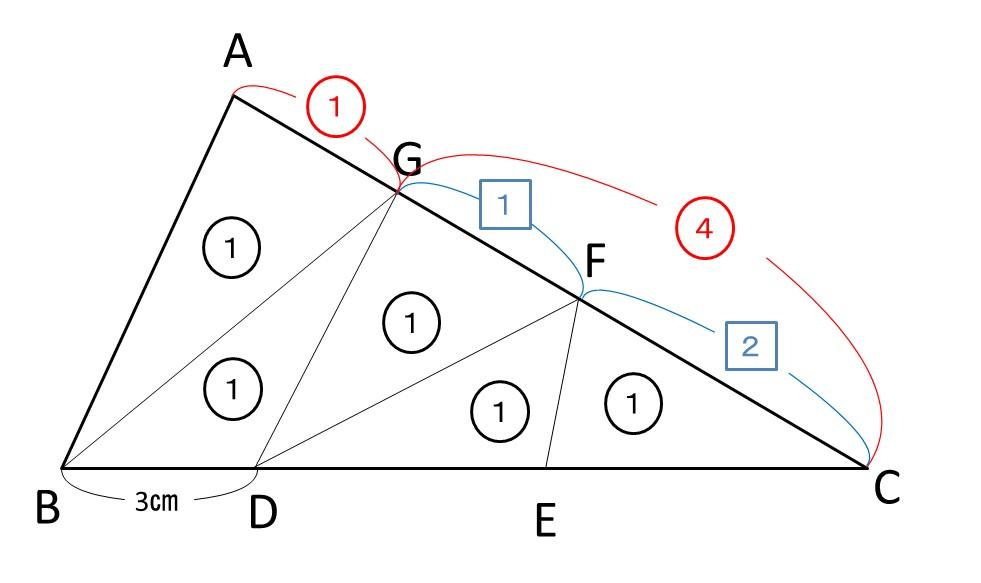
3辺の比　ＡＧ：ＧＦ：ＦＣを求めるには、
同じ辺の長さを2種類の辺の比で表す
連比

まず、三角形ＡＧＢと高さが等しい三角形は、三角形ＧＢＣ　頂点Ｂが共通
ＡＧ：ＧＣ＝1：4

次に、ＧＦとＧＣの比を知りたいので、
三角形ＧＤＦと高さが等しい三角形を探す
三角形ＦＤＣ　頂点Ｄが共通
なので、1：2

比をそろえると、④＝3⃣より、
12にそろえて、
ＡＧ：ＧＦ：ＦＣ＝3：4：8となります。

答え.　3：4：8

ポイントは
高さの等しい三角形を見つける
面積比が底辺比

 

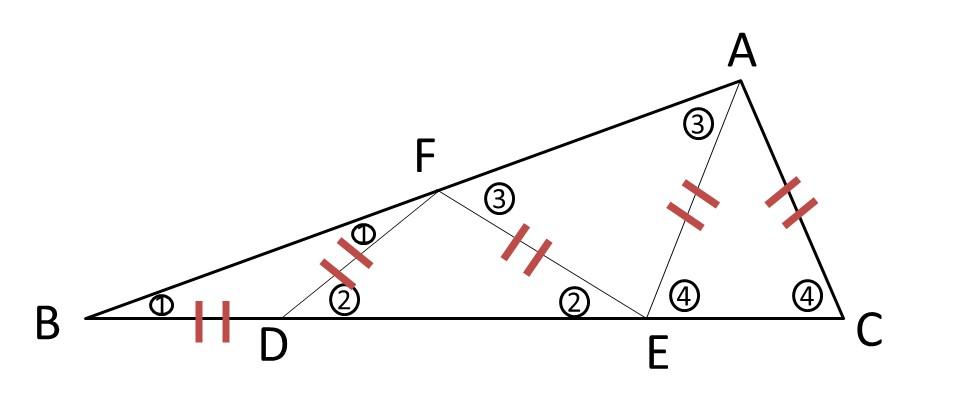
つぎに、【2】は、角度を求める問題でよく出てきます。

問題：
上の図で、辺BD、DF、FE、EA、ACはすべて等しいです。
角FBD＝18°のとき、角AECを求めなさい。

これは、辺の長さが等しいので、二等辺三角形がたくさんできます。
二等辺三角形の性質と、外角の性質を利用するのがポイントです。

 

 

よって、角AECは、18°が4つ分なので、
18×4＝72°

答え.72°

 

いろんな問題を解いていると、これからも
似ている図に出会うことがあるかもしれません。

似ていても、解く解法を間違えないようにしましょう。
そのためには、問題文を正確に読み取るということです。
見た目でだまされないようにするということ。
慎重に解くということを忘れないように。

それではまた、次回。