こんにちは。
受験Dr. の坂井です。
「V形 W形に並べてみよう」の第5弾です。
そのうち、W形についての並べ方について。今回も前回の続きのお話です。
1~7までの数をW形に並べたとき、並べ方が何通りあるかを考えていきます。
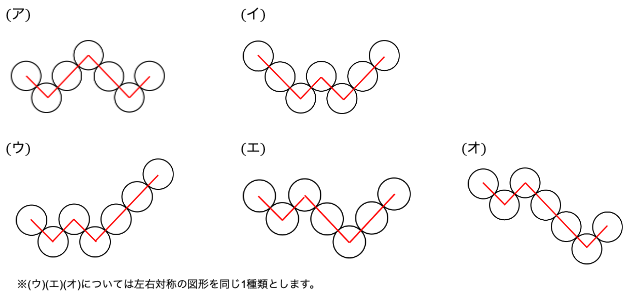
W形の並べ方は次に示すように(ア)~(オ)の5種類の並べ方があります。
並べ方のルールにつきましては、こちらよりご確認ください。
W形の並べ方(ア)~(オ)5種類のうち、これまで(ア)(イ)(ウ)について考えました。
今回は、(エ)の並べ方について考えていきましょう。
(エ)について
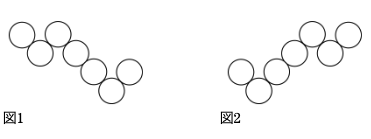
(エ)については、(ア)(イ)が左右対称の形であるのに対し、図1、図2のような2種類の形があることに注意しましょう。
ただし、左右反対の図1、図2の並べ方については同じ通り数ですので、図1についてのみ調べていきます。
並べ方について調べていくときのポイントは(ア)~(ウ)の並べ方について調べたときと同様に
数の位置が限定できるものについて、場合分けをするという点です。
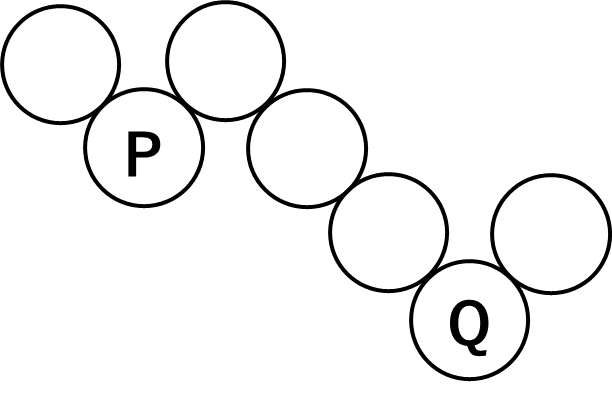
1~7の中で7は最大の数だから、7の位置は
右の図のPまたはQとなります。
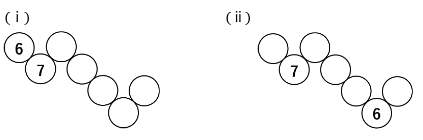
7がPの位置にあるとき
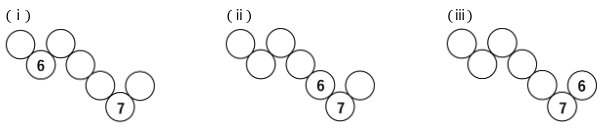
7がPの位置にあるとき、6の位置は次の2通りです。
(ⅰ)と(ⅱ)のそれぞれについて、場合分けをしながら並べ方が何通りあるかを考えていきましょう。
(ⅰ)の場合
1を並べることができる場所で場合分けして考えます。
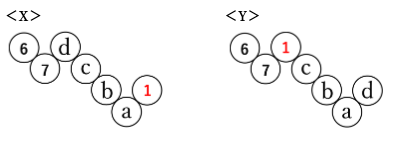
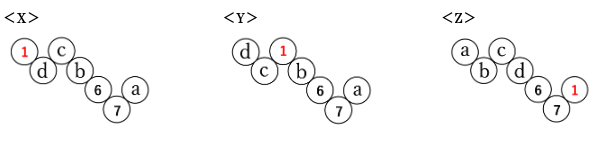
1を並べることができる場所は次に示す<X><Y>の2通りです。
<X>と<Y>の場合について、aの位置に並べる数によりそれぞれ何通りあるかを考えていきます。
<X>について
a>b>c>d になるなるような並べ方は
(a,b,c,d)= (5,4,3,2)のみ よって 1通り になります。
<Y>について
aの位置には5しか並べることができません。
d=2のとき、(a,b,c)=(5,4,3)
d=3のとき、(a,b,c)=(5,4,2)
d=4のとき、(a,b,c)=(5,3,2) よって 1×3=3通り になります。
したがって、(ⅰ)の場合は、 1+3=4通り になります。
(ⅱ)の場合
(ⅰ)と同様に、1を並べることができる場所で場合分けして考えます。
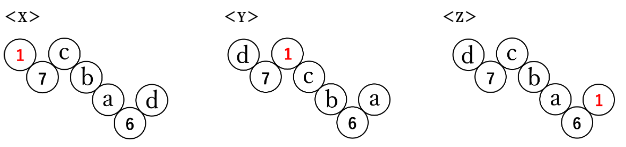
1を並べることができる場所は次に示す<X><Y><Z>の3通りです。
<X>と<Y>と<Z>の場合について、dの位置に並べる数によりそれぞれ何通りあるかを考えていきます。
<X>について
dの位置には2、3、4,5のうち、どの数でも並べることができます。
dの位置に並べた数以外の残りの数は、a>b>c>となるように自動的に並び方が決まります。
d=2のとき、(a,b,c)=(5,4,3)
d=3のとき、(a,b,c)=(5,4,2)
d=4のとき、(a,b,c)=(5,3,2)
d=5のとき、(a,b,c)=(4,3,2) よって 1×4=4通り になります。
<Y>について
aとdは2、3、4,5のうち、どの数でも並べることができます。(a<dでもa>dでもよい)
さらにaとd以外の残りの2つの数は、c<bになるように自動的に並び方が決まります。
すなわち、aとdの並び方(a<dでもa>dでもよい)だけを考えればよいということになるのです。
aとdの並び方: 4×3=12 12通り
<Z>について
<X>と同様にdの位置には2、3、4,5のうち、どの数でも並べることができます。
dの位置に並べた数以外の残りの数は、a>b>c>となるように自動的に並び方が決まります。
d=2のとき、(a,b,c)=(5,4,3)
d=3のとき、(a,b,c)=(5,4,2)
d=4のとき、(a,b,c)=(5,3,2)
d=5のとき、(a,b,c)=(4,3,2) よって 1×4=4通り になります。
したがって、(ⅱ)のときの場合は、4+12+4=20通り になります。
7がPの位置にあるとき、(ⅰ)(ⅱ)より 4+20=24通り となります。
7がQの位置にあるとき
7がQの位置にあるとき、6の位置は次の3通りです。
(ⅰ)~(ⅲ)のそれぞれについて、場合分けをしながら並べ方が何通りあるかを考えていきましょう。
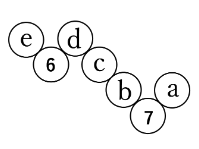
(ⅰ)の場合
1を並べることができる場所で場合分けしてもよいのですが、
今回は、aとeに並べる数に着目して求めてみましょう。
aとeには1~5のどんな数でも並べることができます。
aとeが決まれば、それ以外の残りの3つの数がb>c>dとなるように自動的に決まります。
したがって、(ⅰ)の場合は、aとeの並び方さえ決まればよいので
aとeの並び方: 5×4=20 20通り
(ⅱ)の場合
1を並べることができる場所で場合分けして考えます。
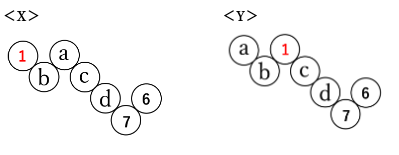
1を並べることができる場所は次に示す<X><Y><Z>の3通りです。
<X>と<Y>と<Z>の場合について、aの位置に並べる数によりそれぞれ何通りあるかを考えていきます。
<X>について
aの位置には2、3、4,5のうち、どの数でも並べることができます。
aの位置に並べた数以外の残りの数の並べ方を、cが最小であることに注意して
考えてみると次のようになります。
a=2のとき、(b,c,d)=(4,3,5)(5,3,4)
a=3のとき、(b,c,d)=(4,2,5)(5,2,4)
a=4のとき、(b,c,d)=(3,2,5)(5,2,3)
a=5のとき、(b,c,d)=(3,2,4)(4,2,3) よって 2×4=8通り になります。
<Y>について
aとbは2、3、4,5のうち、どの数でも並べることができます。(a<bでもa>bでもよい)
さらにaとb以外の残りの2つの数は、c>dになるように自動的に並び方が決まります。
すなわち、aとbの並び方(a<bでもa>bでもよい)だけを考えればよいということになるのです。
aとbの並び方: 4×3=12 12通り
<Z>について
aは2、3、4のうち、どの数でも並べることができます。(aに5を並べることはできません)
aの位置に並べた数以外の残りの数の並べ方を、cが最小であることに注意して
考えてみると次のようになります。
a=2のとき、(b,c,d)=(5,3,4)(4,3,5)
a=3のとき、(b,c,d)=(5,2,4)(4,2,5)
a=4のとき、(b,c,d)=(5,2,3)のみ ⇒ bに置くことができるのは5のみだから
よって 5通り になります。
したがって、(ⅱ)の場合は、8+12+5=25通り になります。
(ⅲ)の場合
1を並べることができる場所で場合分けして考えます。
1を並べることができる場所は次に示す<X><Y>の2通りです。
<X>と<Y>の場合について、aの位置に並べる数によりそれぞれ何通りあるかを考えていきます。
<X>について
aの位置には2以外の数を並べることはできません。(aが3以上の場合、2をどこにも並べることができない)
a=2のとき、(b,c,d)=(3,4,5)(4,3,5)(5,3,4) よって 3通り になります。
<Y>について
aとb(a<b)の並べ方が決まれば、残りのcとd(c<d)の並べ方は自動的に決まります。
aとbの並び方: 4×3÷2=6 6通り
したがって、(ⅲ)の場合は、3+6=9 9通り になります。
7がQの位置にあるとき、(ⅰ)(ⅱ)(ⅲ)より 20+25+9=54通り となります。
以上より7がP、Qにあるときを合わせて、24+54=78通り
そして、図1、図2が左右逆になっていることを考えて、78×2=156通り となります。
みなさん、お疲れ様でした。今回も大変な作業でしたが、もう慣れてきたでしょうか。
次回はついに最終回。(オ)を扱っていきますので、是非チャレンジしてみてください。
ポイントは、まず7の場所について場合分けをすることです。さらにそれにつながる6の場所が限定されるので6について場合分けをし、最後に最小の1について場合分けをして集計をしていくことです。一言で言えば、数の位置が限定できるものについて、場合分けをしていくということになります。
それではみなさん、
またお会いしましょう。