みなさん、こんにちは。
算数・理科講師のM.S.です。

2月になり、新年度を迎えた方も、これから迎える方もおられると思います。

本日は、算数の勉強についてお話をしたいと思います。

算数の勉強はスポーツの練習と似ていると思います。
スポーツの練習では、常に実戦形式の練習試合をしているスポーツはあまりないです。
多くの練習はシチュエーションに合わせた練習を繰り返し、繰り返ししています。
例えば、柔道であれば背負い投げばかり練習したり、野球であればバッティング練習ばかりしたりとそのシチュエーションごとの練習をして、実戦的な練習をしています。

算数でも同じで、まず例題でその回の核となる基本的な解法を練習してそれができるようになってから、練習問題、応用問題と進むことになります。
練習問題や応用問題は基本問題からひとひねり、ふたひねりされているので、基本的な解法にひと手間、ふた手間加えて解くことになります。
その手間の加え方も練習がいるので算数は大変ですね。

算数が得意でないお子さんの場合、基本的な解法が習得できていなかったり、手間の加え方を覚えられなかったりと様々ですが、しかしそのどこでできていないかを見てあげることでできるようになっていきます。

また、お子さんによって習得時間に差があります。
基本的な解法も手間の加え方もサッとできるお子さんもおられれば、基本的な解法はサクッとできるようになるけれど、手間の加え方の方はなかなかできるようにならないという子もおられます。
そして、基本的な解法が習得できないが、それができたらあとは進むお子さんもおられますし、解法も手間の加え方も時間がすごくかかるお子さんもおられます。

基本的な解法が習得に時間のかかるお子さんは基本問題を繰り返すことが大事に、手間の加え方が苦手なお子さんは練習問題を繰り返すことが大事になると思います。
ですから、宿題で算数の問題がわからないといっても対策が変わってくるので、お子さんがどの場面までできているのかを見てあげることが本当に大事だと思います。

躓いた箇所の探し方をお話しできればと思います。

過不足算です。
様々な解き方がありますが、2つほど紹介します。

＜解き方①＞
子どもの数を□人とすると、

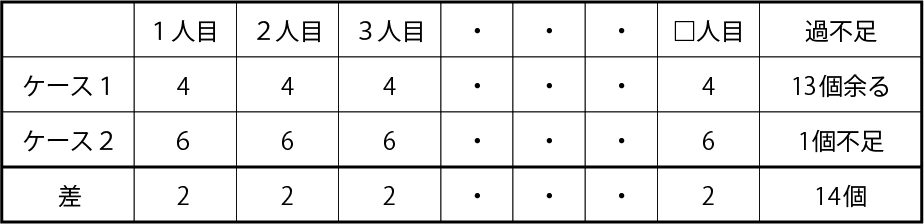
これから、
□人＝14個÷2個＝7人となります。

＜解き方②＞
4個ずつミカンを配ったときのミカンの個数を④とする、6個ずつミカンを配ったときのミカンの個数は⑥と表せます。これから、ミカンの個数を式で表すと、

④＋13個＝⑥－1個　　となり、
②＝14個から　　①＝7人　となります。

これ以外にも、面積図や線分図などがあり、塾によって、はたまた、先生によって、習ってくる解き方が違うと思います。
躓いた箇所を探すときは、まず、表が書けているのか？立式できているのか？など、
問題を読んだ後に、手が動かせているか確認します。
それができていない場合は、表を書くのみ、式を立てるのみしてみてください。
これができていれば、答えの求め方を練習してみてください。
つまり、解答までの手順をできるだけ細かく分け、そのひとつひとつを練習してください。

野球のバッティングでいう、バットの握り方、構え方、タイミングの取り方、バットの振り方などをひとつひとつ確認していくのと同じです。

そして、基本的な問題ができたときには、次のステップです。

練習問題になったときには、まず基本的な問題との違いを考えます。
そして、次にその違いをどのように対応すれば解けるかを考えます。

問題２では、問題1と違って1回の配り方に、2種類の個数があります。
これにまず気づけるでしょうか。
気づけなかったときには、一緒に考えて、ヒントを出しながら、誘導してみてください。
気づけたとき、1回の配り方を1種類にしたいなぁ～、どうしたら1種類になるか対応を考えます。

この場合、男子1人と女子1人を1組として考えます。つまり、
・『男の子には1人2個ずつ、女の子には1人に4個ずつ配る』
→『男子1人と女子1人の1組に6(＝2個+4個)個ずつ配る』
・『男の子には1人3個ずつ、女の子には1人に5個ずつ配る』
→『男子1人と女子1人の1組に8(＝3個+5個)個ずつ配る』　となります。

すると、ここで、一つ問題が新たに発生します。これにも気づけるか確認が必要です。
問題というのは、女子と組になれなかった男子3人の処理です。
この男子3人には配らず、あめ玉を返してもらい、あまりと不足をもう一度計算します。

ケース1の場合:30個＋2個×3人＝36個あまる
ケース2の場合:3個×3人－3個＝6個あまる

このような手間を加えると、問題2が問題1と同じように解くことができます。
そして、練習問題はこの手間だけ覚えておくと、解法を一から覚えるより効率的です。

ちなみに、

＜解き方①＞
子どもの数を□人とすると、

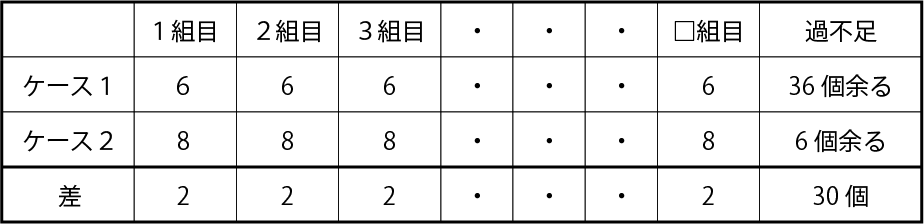
これから、
□組(女子の人数)＝30個÷2個＝15組(人)となります。

＜解き方②＞
6個ずつアメを配ったときのアメの個数を⑥とする、8個ずつアメを配ったときのアメの個数は⑧と表せます。これから、アメの個数を式で表すと、

⑥＋30個＝8＋6個　　となり、
②＝30個から　　①＝715組(人)　となります。

そして、アメの個数は
2個×(15人＋3人)＋4個×15人＋30個＝126個
3個×(15人＋3人)＋5個×15人－3個＝126個

最後に、算数は不得意なお子さんにとってはできるようになるまで時間がかかる教科だと思いますが、問題とその解き方をまるまる覚えるのではなく、躓いているところを探して練習するだけで、丸覚えよりは覚える量が少なく楽にできるようになると思いますので、試していただければ幸いです。