みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。
前回のブログで、N進法についての問題を紹介いたしました。
今回は、今年の入試問題からN進法の問題を紹介いたします。
⓪=1円相当、①=3円相当、②=9円相当、③=27円相当・・・のように書かれた数字が1増えるごとに相当金額が3倍になる仕組みになっています。この角コインを1枚ずつ持って買い物をするとき、次の問いに答えなさい。ただし、おつりにおいても同じ種類のコインは1枚ずつしかなく、やりとりするコインの総数も出来る限り少なくなるようにするものとします。
(a)省略
(b)2022円の品物をこのコインで買うことができますか。出来る場合はそのコインのやりとりを具体的に答え、出来ない場合は×を書きなさい。
[駒場東邦 2022]
[解説]
各コインの金額は以下のようになります。

⑦のコインを使用すると
2187-2022=165円
となります。おつりにおいても各コインを1枚までしか使うことができません。
よって、どう頑張ってもおつりの165円を作ることができません。
(コイン番号⓪~④を足しても121円となり、165円に届きません)
よって、支払う金額を調整し、おつりを支払えるようにします。
支払うコインを⑦のコイン+別のコインと考えると、おつりは以下の表のようになります。
◆追加するコインとおつりの関係

④のコインを追加した際のおつりの246円は、①のコインと⑤のコインで作ることができます。
よって、④と⑦のコインで払い、おつりを①と⑤のコインでもらうことで2022円の品物を買うことができます。
と、整理して解くこともできます。
しかし、この問題が3進法と関わりが深いことを見抜くことができると非常に考えやすくなります。
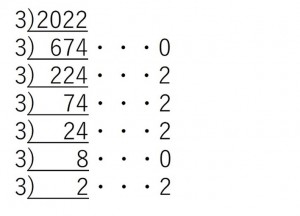
より、2022を3進法に変換すると2202220となります。

以下のように点線部分で2つに分けます。

下4桁の「2220」は、①のコインを1枚追加すると繰り上がって「10000」となることに気が付きましたか?
つまり、「2220」の部分は④のコイン1枚を支払い、①のコイン1枚をおつりとしてもらうことで支払い可能です。
「220」についても同様です。⑦のコイン1枚を支払い、⑤のコイン1枚をおつりとしてもらうことで支払い可能となります。
よって、④、⑦を使い、①、⑤をおつりとしてもらうことで2022円の品物を買うことができます。
前回同様、N進法に変換することで作業量を大幅に削ることができます。
ご参考になれば幸いです。
それでは、今回はここで失礼いたします。
受験ドクター 川上亮




