皆さんこんにちは。
受験ドクター講師の勝山利信です。

今回は問題対応力の鍛え方についてお話しします。
以前に「同じ事実の言い換え」についてお話ししましたが、今回は問題文もストレートに条件を与えているのに同じように見える問題が同じようには解けなかったり、解き方は分かっているがなぜそのような解き方ができるのかはよく分かっていなかったりと苦戦しているお子さんもいることでしょう。

そのような場合、問題を解くときの姿勢が一問一問に対して一つ一つ解き方を覚えようとしてしまい、高学年になるほどに手一杯になってしまうこともあります。覚えるべきこともありますが、理解を深め様々な応用的な問題に対応できる力を身につけていければ理想的ですね。

さて、そのような力を身につけるために、食塩水に関する問題を扱っていきたいと思います。
食塩水の濃さに関する問題で、大元の考え方になるのが三用法とも言われる関係式ですね。

3つの要素の内2つが分かれば、最後の1つも計算ができる関係になっています。
初歩的な問題であれば、式を正確に覚えて使用できれば正解できるでしょう。
しかし、式をしっかり学習していても、ちょっと考えさせられる問題が次のような問題です。

シンプルな問題ですが、さぁ式を使って計算するぞ、と手を動かそうとすると一度止まります。
混ぜた食塩水の量が分かっていないので、出来上がる食塩水の量も分かりません。
一方が分かればもう片方も分かるという関係性なので、普通に計算しようとすると上手くいきません・・・。

ご家庭ではお子さんから解き方を問われたときに、方程式を使って説明することもあると思います。
方程式を使うことを否定はしませんが、算数のための応用力を身につけたい場合は、次のようなイメージ図を上手に活用しましょう！テキストにもよく載っている図ですが、なぜそのような図で解決できるのか、理解も同時に深めていければベストです。

先ほどの三用法の式②より、この3つの要素を長方形の縦の長さ、横の長さ、面積に照らし合わせます。

すると、先ほどの問題の状況は次のような図でとらえることができます。

そして、ここが最も重要なのですが、算数では「等しさ」を利用して物事を考えていくことが基本姿勢になりますので、図の中で等しい部分はないか考えます。
今回の「等しさ」は、混ぜる前後で食塩の合計量（図における面積）が変わらないということです。

さらに、その等しさを生かすために、混ぜる前後の図を重ねます。最初から重ねた状態で図を書いて説明しているテキストも多いので、ご家庭でお子さんの学習をサポートするのであれば、重ねる前の図を一緒に考えてあげるとスムーズです。重ねてみると、元の面積が等しいのでアとイの長方形の面積が等しいことが分かります。

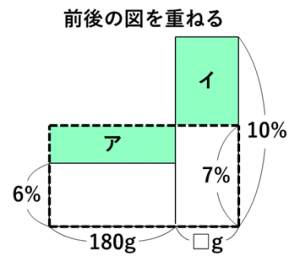
アの面積は(7－6)×180＝180ですから、イの面積も180です。
イの縦の長さは、180÷(10－7)＝60となるので、10％の食塩水を60g混ぜたことが分かります。

学年が上がると、具体的な量ではなく、比率で条件が与えられることもありますが同じ考え方で解決できます。売買損益の問題でも、売り上げを面積でとらえることで同じように解決するともできますね。また、理科でてこの原理を学習してからは、てんびんの図でまとめることもさらに簡略化できて効果的です。

算数では様々な図を使って理解を深めていきます。使っているうちに、そもそもなぜそのような図で表して考えることができるのか忘れてしまいがちですが、応用的な問題ほど基本に立ち返って考えることで解決の糸口が見えてきます。次回は実際に応用する問題についてお話しします。

目指せ問題対応力UP！
それでは、またお会いしましょう！