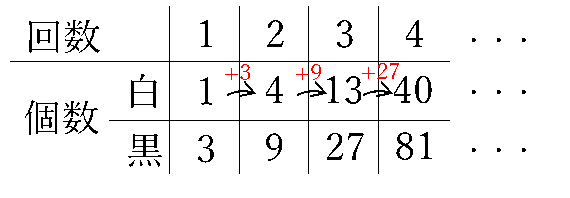こんにちは、受験ドクターのK.Dです！

今回はタイトルにもあるようにシェルピンスキーのギャスケットというフラクタル図形の一種について触れたいと思います。

まず、シェルピンスキーのギャスケットと聞いて、どんな図形か想像がつく方はいるでしょうか。

まずいないと思います。正直、私もこの業界で働いていなければまず知りえなかったでしょう。

では、早速ですが、シェルピンスキーのギャスケットの問題です。

（問）下の図のように正三角形があり、「正三角形の各辺の中点を互いに結んでできた中央の正三角形を白く塗る」という作業を永遠に繰り返すとき次の問いに答えなさい。

（１）3回目の操作をしたとき、黒い三角形と白い三角形の面積比を求めなさい。

（２）4回目の操作をしたとき、黒い三角形と白い三角形の個数の比を求めなさい。

（３）5回目の操作をしたとき、黒い三角形と白い三角形の面積比を求めなさい。

（４）6回目の操作をしたとき、黒い三角形と白い三角形の個数の比を求めなさい。
 
 
どうでしょう。できましたでしょうか。（１）と（２）あたりまでは実際の図から求められたかもしれません。ちなみに（１）の答えは、27：37で、（２）の答えは81：40です。

（３）、（４）は実際に図を描いて考えるのはかなり厳しいと思います。
そこで、この図形の規則を考えてみましょう。
 
2つ前の記事でどんな数列になっているか分からない（そもそも規則のある数列になっているかも分からない）けど、とりあえずいくつか書き出してみることで規則を発見しようと書きましたが、今回も同じく、書き出して考えてみましょう。

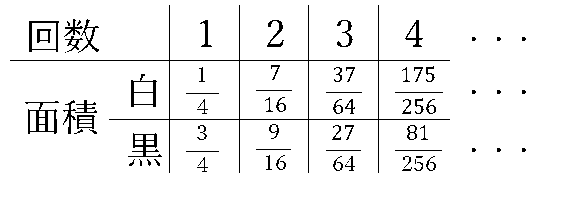
面積について書き出すと上記のようになります。黒い三角形の面積の合計に着目すると、1回目の操作でになり、2回目の操作でさらにになっていることが分かります。
すると、白い三角形の面積の合計は全体から黒い三角形の面積の合計を引いたものになります。

よって、5回目の操作で黒い三角形の面積の合計：白い三角形の面積の合計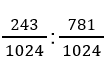＝となります。

つまり、（３）の答えは243：781となります。

次に、個数について書き出してみましょう。

白い三角形の個数は+3、+9、+27、+81、+243と増えるので、6回目の操作を行った後の白い三角形の個数は364個と分かります。

黒い三角形の個数は3の平方数になっているので、6回目の操作を行った後の黒い三角形の個数は3×3×3×3×3×3＝729個と分かります。

よって、（４）の答えは729：364と分かります。

今までは、入試において知っておかなければいけない知識についての記事が多かったですが、入試も一段落着きましたので今後はこのように少し変わった内容の記事も書いていこうと思います。

それではまた。