みなさん、こんにちは。受験Dr.の亀井章三です。
今回も時計の長針と短針が成す角度を考える時計算という問題についてです。
時計算は旅人算の特殊算とも言われており、やや難しい問題です。
その時計算の解き方を整理していきたいと思います。

 

１　時計の動きの基本情報の確認

時計算で出てくる長針（分針）と短針（時針）の動きは決まっています。毎回計
算して求めていては大変なのでおぼえてしまいましょう。
　長針（分針）　1時間で1周＝60分で360度＝分速6度
　短針（時針）12時間で1周＝720分で360度＝分速0.5度
また、旅人算では兄と弟が同じ方向に進んだり、反対方向に進んだり、と動きは様々ですが、時計の針は文字通り時計回りにしか進みません。
そのため、1分間で長針は短針より5.5度多く進むことになります。この速度の差も毎回使いますのでおぼえましょう。

 

２　両針の作る角度が90度になる時刻を求める

ここからが本題です。
問題　4時と5時の間で時計の長針と短針の作る角度が90度になるのは、
4時何分ですか。全て求めなさい。
この問題について考えてみましょう。今回のテーマも解法のパターン化です。
ただし、どんな時刻でも共通して使える一つの公式というものは作れません。したがって、今回の内容はパターン化の応用とも言えるでしょう。
前回は「2つの針が重なる（作る角度＝0度）時刻」と「2つの針が反対方向に一直線になる（作る角度＝180度）時刻」を考えました。
その問題文と、今回の問題文で大きく異なるのが、「全て求めなさい」です。

0度と180度は指定された1時間の中に１回しかありません。
しかし、90度は2回以上あるということです。そこで90度になる時刻がいつ現れるかを考えます。

4時と5時の場合、最初の4時ちょうどの時点で2つの針の作る角度は120度です。
これが時間とともに小さくなっていきます。

ということは、120度から0度になる間に「1回目の90度」が訪れます。
重なったあとはどんどん広がっていき、やがて反対方向に一直線となる180度になります。
そうすると、この間に「2回目の90度」が訪れます。

反対方向に一直線になったあとは、間の角度は狭まっていきます。
そして、最後5時ちょうどになったとき150度になります。

この角度の流れをまとめると、
120度→90度（1回目）→0度→90度（2回目）→180度→150度
となります。

では、時刻を求めます。1回目は4時ちょうどの角度から30度狭まっています。
したがって、 これが1回目の90度です。
2回目は、4時ちょうどの時の120度が狭まり0度になる。その後90度広がった
ので、合計120＋90＝210度長針が多く進んだ時です。
　これが2回目の90度です。

よって、答えはの2つです。
ではこの問題をパターン化しますが、ここである問題が生じました。

それは、与えられた時刻によって、「針が重なる」「反対方向に一直線になる」「1回目に90度になる」「2回目に90度になる」の順番が異なるということです。

具体的に表にまとめると次のようになります。

 

 

＜１＞最初の時刻が0時・1時・2時の場合

1回目の90度は、重なってから90度広がるまでの時刻です。つまり、
（30×〇＋90）÷5.5　を計算することで時刻が求まります。
2回目の90度は、反対方向になってから90度狭まるまでの時刻です。つまり、
（30×〇＋180＋90）÷5.5＝（30×〇＋270）÷5.5　を計算することで時刻が求まります。

 

＜２＞最初の時刻が3時・4時・5時の場合

1回目の90度は、最初の状態から90度まで狭まった時です。つまり、
（30×〇－90）÷5.5　を計算することで時刻が求まります。
2回目の90度は、重なってから90度広がるまでの時刻です。つまり、
（30×〇＋90）÷5.5　を計算することで時刻が求まります。

 

＜３＞最初の時刻が6時・7時・8時の場合

1回目の90度は、最初の状態から反対方向に一直線になり、その後90度狭まっ
た時です。つまり、
（30×〇－180＋90）÷5.5＝（30×〇－90）÷5.5　を計算することで時刻が求まります。
2回目の90度は、重なってから90度広がるまでの時刻です。つまり、
（30×〇＋90）÷5.5　を計算することで時刻が求まります。

 

＜４＞最初の時刻が9時・10時・11時の場合

1回目の90度は、最初の状態から90まで広がった時です。つまり、
（30×〇－180－90）÷5.5＝（30×〇－270）÷5.5　を計算することで時刻が求まります。
2回目の90度は、反対方向に一直線になってから90度狭まるまでの時刻です。つまり、
（30×〇－180＋90）÷5.5＝（30×〇－90）÷5.5　を計算することで時刻が求まります。

 

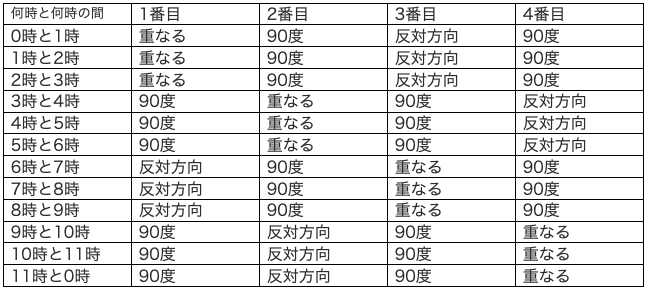
表にまとめると、

 

この公式自体をおぼえる必要はありません。大切なのは、共通点を見つけ、式に
落とし込むということが、全体の把握に役立つということです。

 

３ 両針の作る角度が□度（□は0、90、180以外）になる時刻を求める

時計算の問題も最後になります。
それは、ここまで話してきたパターン以外の角度になる時刻です。これは最初の時刻や求める角度によって様々なため、パターン化するのはかなり困難です。

そこで解法作業のパターン化を行います。解法作業のパターン化とは、公式を作るのではなく、行う作業を一つにまとめるというものです。

今回の場合は、②の解説でも行った「針が重なる」「反対方向に一直線になる」「1回目に□度になる」「2回目に□度になる」の順番を考え、そこから長針が何度多く進めば良いかを考えるというものになります。
この方法を用いれば、どのような条件でも計算式を正しく作ることができます。

 

3回に渡って時計算とパターン化の話をしてまいりました。
このテーマは今回で終了です。

このパターン化の考え方は全ての算数の問題に適用することができますので、また改めて他の単元のパターン化についてもお話ししたいと思います。