みなさま、こんにちは。
受験ドクター算数科のHH講師です。

本日は、立体切断の3つの基本についてお伝えしたいと思います。

【3つの基本】
その1　同じ面にある点を結ぶ
その2　向かいあう面の切り口は平行
その3　延長する

この3つで、切断面がどのような形になるのかを見分けることが出来ます。
切断面がわからず悩んでいるお子さんの大半は、これで解決します。

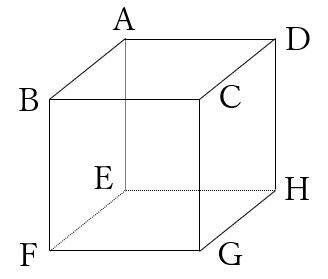
具体的に下の図のような立方体で説明します。

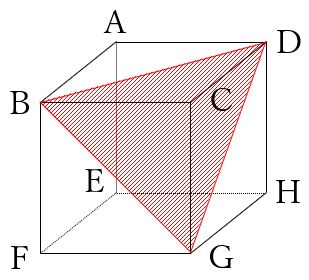
(1) 頂点BDGを通る平面で切断。
頂点BD、頂点BG、頂点DGはそれぞれ同じ面にあるので、線で結びます。

図のように、切り口は正三角形となります。(全ての辺の長さが等しい)
3つの基本、その1を使って切断面を見極めました。

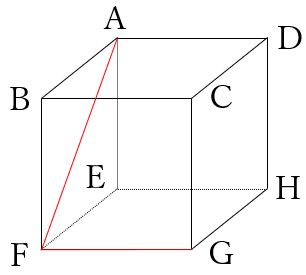
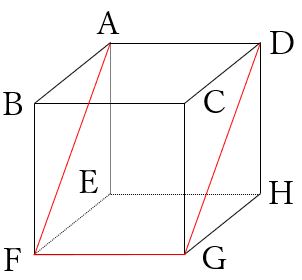
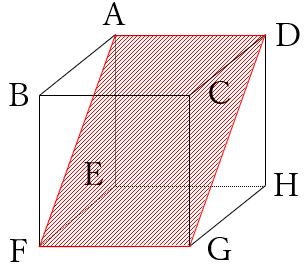
(2) 頂点AFGを通る平面で切断。
頂点AF、FGはそれぞれ同じ面にあるので、線で結びます。

次に、面ABEFと面DCGH(向かい合う面)に着目し、点Ｇを通りAFに平行な線を引きます。

さらに、点Aと点Dは同じ平面上にありますので、線で結びます。

図のように、切り口は長方形となります。
3つの基本、その1→その2→その1を使って、切断面を見極めました。

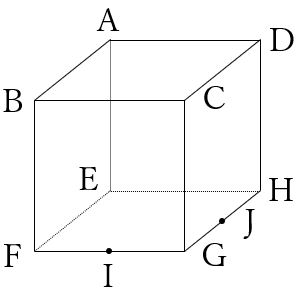
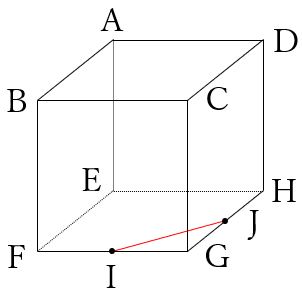
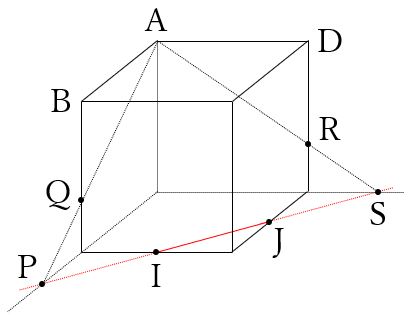
(3) 以下の図の、点ＡＩＪを通る平面で切断(点Ｉと点Ｊは各辺の中点)。

点Iと点Jは、同じ平面にあるので線で結びます。

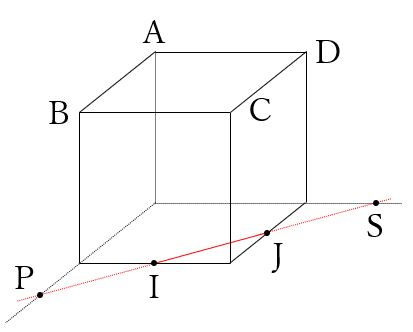
その1．その2は使えませんので、その3を考えます。
線分ＩＪと、辺EFと辺EHを延長し、交わる点を見つけます。

それぞれ交わった点をPとSとします。
次に、点PとSから頂点Aに向かって線を引きます。
立方体の辺と交わった点をQとRとします。

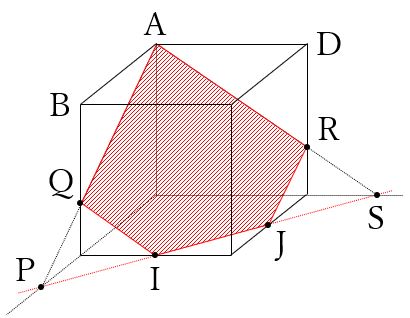
点AとQ、点QとI、点JとR、点RとAをそれぞれ線で結ぶと切断面が出来上がります。

図のように、切り口は五角形となります。
3つの基本、その1→その3→その1を使って、切断面を見極めました。

このように、3つの基本を使いこなせば切断面を見極める事ができます。
実際の入試問題では、切断面を考えた後に体積や表面積を求めさせる問題がほとんどです。
切断面がわからなければ体積も表面積も求められませんので、切断の3つの基本を覚え、使いこなせるようトレーニングを行いましょう。

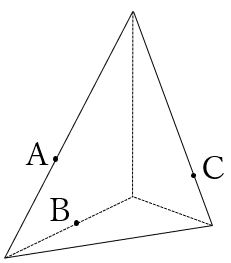
最後に、すい体もこの考え方で切断できますので、お見せしたいと思います。
例）下の三角すいを点A・B・Cを通る平面で切断しました。切断面を作図しなさい。

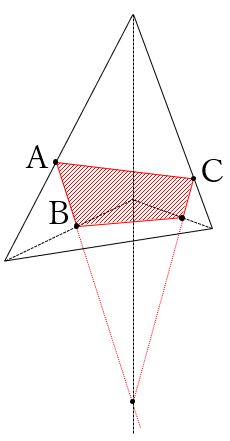
すい体になると、向かい合う面が平行ではなくなるので、切断の基本その2が使えなくなります。その変わり、その3を使う場面が多くなります。

このように、切断面は四角形となります。

いかがでしたでしょうか？
立体切断と聞いて、難しいように感じるかもしれませんが、基本は3つです。
切断のトレーニングを行う場合、慣れるまではスペシャリストをとなりに置いて行うようにしましょう。誤った切断方法に慣れてしまうと、後々修正するのが大変です。
3つの基本が使えるようになれば、どんな形でもバッサリと切断できるようになりますよ。

では次回、またお会いしましょう。