こんにちは！
受験ドクター算数科のRS講師です。

いよいよ受験まで本当にわずかです。
受験ドクターの各校舎では、受験生たちが最後の追い上げで頑張っています。

みんながそろって合格を勝ち取れるように、初詣のお願いに行ってきました。
私の担当の生徒たちの顔を一人一人思い浮かべながら、長い間手を合わせていたので、一人で随分と神前を占拠してしまいました（^^;

さて、受験直前期だけどお話の内容は四年生向けです。
テーマは「四捨五入」

いま6年生たちが取り組んでいる問題の難しさに比べれば、なんてことないお話ですが、四年生の最初の最初にならうテーマとしては結構難しいと感じる子が多いところです。
特に、「四捨五入して5400になるのは、〇〇〜〇〇までです」のような問題で、混乱するケースが多いので、新年度開始の前にちょっとしたコツをお伝えしておきたいと思います。

私がブログを書くと、どうしても「〇〇とは、何ぞや？」という話が多くなってしまうのですが、そこは我慢してお付き合いください。

さて、そもそも四捨五入とはなんのためにあるのでしょうか？？
皆さん、自分の身長や体重は分かっていますよね。
小学生のお子さんだったら、身長は130cm〜150cmの間ぐらいでしょうか。
私の場合、身長は170cmぐらい、体重は・・・内緒です。
はい。ここに実はすでに四捨五入が使われているのが分かりますか？

私の身長は正確には173cmなのですが、いま170cmぐらいとお伝えしました。
わたしの身長をイメージしてもらう上で、3cmという細かな部分はあまり重要な情報ではありません。
かといって、私が（170cmだから、200cmに近いな・・・）と思って、「私の身長はだいたい200cmです」とお伝えしてしまうと、「え？やばい。でかすぎ。柴田先生はNBA（アメリカのバスケットリーグ）の選手なんですか？」ってなりますよね。
誰かに数字を伝える際に、どれぐらいの細かな情報までを伝えるのか？というのはとても重要なことだと分かります。大雑把すぎると間違ったイメージを伝えかねませんし、逆に細かすぎても大事なポイントがボヤけてしまうことがあるのです。

このように、どれぐらいの細かな情報までを伝えるか？を決めるのが四捨五入の考え方で大事な部分です。
100の位までの情報でよければ、「10の位を四捨五入し、100の位までのがい数」となりますし、100の位を四捨五入すれば、「1000の位までのがい数」となります。
10の位までのがい数では、0に近いものは無いものとみなし、10に近いものは10に満たなくても10とみなします。先程のケースだと、3cmは0に近いので無いものとして（切り捨て）、もし9や8ならば10と考えてしまおう（切り上げ）ということになります。
0，1，2，3，4，5，6，7，8，9の10個の数字の丁度真ん中が、4と5の間にあるので、4までは切り捨てて、5から上は切り上げる、というのが四捨五入のルールとなるわけですね。

さて、ここまでは四捨五入の当たり前の考え方ですが、
今日お伝えしたいのは、冒頭でもお伝えした「四捨五入して〇〇になるのは〇〇〜〇〇」という問題をお子様に解りやすく教える方法です。

こんな問題で考えてみましょう。

【問い】100の位までの概数で表すとき、3000になるのは□以上、□未満の数です。

↓
↓
↓
↓
↓

〈考え方〉
この問題は、テキストにはあまり詳しい解説がないことが多く、「2950以上〜3450未満」と答えだけが載っているようなケースも珍しくありません。
大人にとってはぜんぜん難しくないのですが、お子さんによっては、2500〜3400とか答えたりと、桁の概念が弱いとすぐに混乱を起こしてしまいます。

はい、それでは受験ドクター流の教え方を披露しましょう。

ある国の王さまが、突然こんな風に言いました。
「1円玉や、10円玉のような細かいお金は財布が重くなるし、私は細かなお金をちまちま払うのは大嫌いだ。だから明日から1円玉や10円玉（ついでに5円玉も）は廃止して、100円玉をこの国で一番小さなコインということにするぞ」

突然、100円玉より細かなお金がない国になってしまいました。

さあ困ったのはこの国の国民達。
パン屋さん「うちの120円のパンは明日から何円にすればいいんだろう？」
八百屋さん「273円で売っていたかぼちゃがあるんだが、明日から何円にしようか？」

こんなふうに考えてもらうと、たぶんお子さんたちは、迷うことなく「パンは100円、かぼちゃは300円」と答えてくれると思います。

ポイントは、100の位までの概数＝100円がもっとも細かな硬貨　というところに置き換えてしまうことです。
これこそが、100の位までの概数で表される世界です。

そして、ここで線分図によるイメージ化を行います。

273円のかぼちゃが300円になる話しでいきましょう。
線分図を書いて、300円を真ん中の目盛りとします。

300円の左右の目盛りはなんでしょうか？299と301？295と305？
でも、この国には100円より細かなお金はなくなってしまったのです。

ということは、300の左右の目盛りは200と400です。

でも昨日までは273円という金額でかぼちゃを売っていたのですから、
これを300円にするか、200円にするか決めないといけません。

 
273円が300円になる理由がこれでハッキリとします。

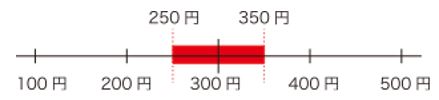
つまり、10円や1円がない世界では、200円と300円の間にある数字はその真ん中の250を境目にして200円か300円かを選ぶわけです。300円と400円の間も同様です。
従って、300円という概数になる範囲は、250円以上〜350円未満となります。
「以上」と「未満」の概念がまだ理解できていないお子さんの場合は、350の一つ手前の349までと補足してあげて下さい。

さて冒頭のお話ですが、100の位までの概数で表したときに3000になる範囲は、

①この国の最も大きな数字の単位は何かを確認する。→今回は100

②3000を真ん中に書き、左右に2900と3100を書く

③2900と3000の真ん中、3000と3100の真ん中にそれぞれ印をつけて2950と3150をそれぞれ書き込む。

④答え 2950以上3150未満とする。

この手順で何問か繰り返し演習することで間違いなくしっかりと出来るようになるはずです!
ぜひお子様と実践してみて下さい。

本日はコレにて。ではでは(^o^)/~~~