みなさんお元気ですか？！
受験ドクター算数科のRS講師です。

最近ホント寒くなってきました。
これから受験本番というのに風邪を引いてしまいそう・・・。
受験生の皆さんも体調管理には十分気を付けて下さいね。

さて、今回は前回の内容の応用編といきましょう。
前回は、〇5✕〇5　や　〇3✕〇7　などの十の位が同じで、一の位の和が10となっている2桁のかけ算についてのテクニックを紹介しました。
その完成編ということで、すべての2桁✕2桁のかけ算に対応できるインド式暗算です。
さすがに、前回のような単純なものとはいきませんが、まずは次の例を見て下さい。

例：83✕24

手順：
①　十の位どうし、一の位どうしをかけます。
　　8✕2＝16、3✕4＝12
②　これを横に並べます。1612
③　次に互いの数の十の位と一の位をかけます。
　　8✕4＝32、2✕3＝6
④　③で計算した数を十の位の位置に右揃えでならべて、最初の1612に順に足していきます。
　　ここでは、61＋32＋6＝99（実際は610＋320＋60 の意味）
⑤　答えが1992となります。

はい。かなり難しいですね・・・
「てか、フツーにやった方が速いよ！」という声も聞こえてきそうな感じです(^_^;)
まあ、そこはグッとこらえて最後までお読み下さい。

まあ、とりあえず文だけでは分かりにくいと思うので、
上記を図解してみましょう。
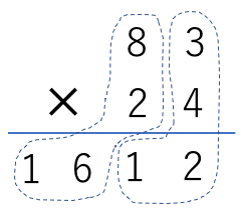
手順①、②

こういうことですね。これは簡単だ！
ここで終わりだったらいいのに・・・（笑

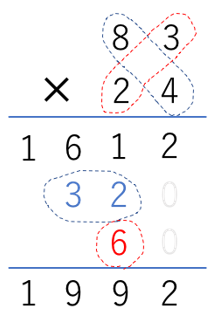
手順③、④、⑤

なるほど。図にしてみると、やってることはシンプルですね。
原理を説明しましょう。

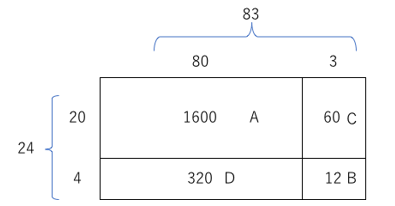
83✕24を図のように長方形の面積として考えます。
このとき、83を80＋3、24を20＋4 として考えると、
長方形の面積は、上のように4分割された長方形の面積の合計として考えることが出来ます。
手順①の計算は、このうちの1600と12をそのまま並べたものです。
Bの部分は、もっとも大きい場合でも9✕9＝81なので、A＋Bの計算時には、繰り上がりは絶対に起こらないということが言えます。だから、手順①、②は横に並べるだけでいいのです。これは利点と言えますね。

そして、残ったCとDの部分ですが、これは互いの数の一の位と十の位をかけたものどうしです。
十の位の数をかけているから、ゼロがお尻に1つつくので、1の位をあけているわけですね。
あとは、足すだけです。

いかがでしょうか。
通常の筆算だと3桁どうしの足し算となる場合が多いので、頭の中だけのイメージは少々辛いものがありますが、
この計算だと、2桁の数を3つ。上手くまとめられることも多いので、2桁の足し算を2つですむ場合が多くなります。脳内イメージだけでもなんとかなりそうな感じ・・・。
（手順③〜⑤のときに、3桁に繰り上がるとちょっと難しくなってしまいますが・・・）
手順だけで比較すると、通常の筆算とインド式と賛否両論がでてくると思うのですが、上記のように長方形を4つの部分に分けて考える問題というのが中学入試では時々出題されます。この方法はその着想と近いものがあるので、この方法に慣れておくのはひとつのメリットです。

また、このように別の方法をマスターしようとすると、普段使っていない脳の部位を刺激することになります。
目をつむって目の前の空間に数字を思い浮かべてみて下さい。
普段使っていない脳の部位が全力で回っている感じがしませんか？・・・私はします(^0^)

人間の“脳”力は、いままで使ってこなかった部位を刺激することで上がっていくものです。
普通の筆算はみなさんマスターしているでしょうから、さらなる脳力アップを目指して、新しい方法に挑戦してみることもいいかもしれませんよ。

さて、2回に渡ってインド式暗算をご紹介しましたが、実はインド式暗算は紹介した以外にもいろんなパターンがありますが、分配法則や、25✕4の工夫などを利用したパターンなど、中学入試でよく出てくる考え方を応用したものがほとんどです。
「前回の内容」＋「一般的な計算の工夫」だけでも結構楽に計算出来るようになりますから是非とも普段の勉強に取り入れて見て下さい。

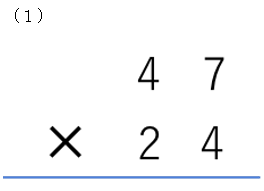
最後におまけの練習問題

今回はここまで。
ではでは〜^^

答え：（１）１１２８（２）１９４４（３）２０１６