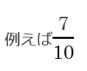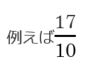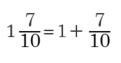算数・理科担当の大木快です。

テストでミスが多い、というお悩み、多いですね。原因は人それぞれですが、計算ミスに関していうと、ミスしやすい場所は…
分数。

どんなに苦手なお子様でも、小６になって分数ができない、ということはまずありません。（怪しいな、ということはありますが）

でも、初めて習う時の大変さといいますか、産みの苦しみといいますか…楽な道のりではなかったはず。たとえば

分数÷分数

の意味が正しくイメージできるかというと、大人でも難しい。面倒くさいので、結果だけ覚えてしまった方が楽だったりしませんでしたか。

イメージ不十分で詰め込むと、どっちがどっちだったかあやふやになるということが起こります。繰り返して上手になっていくものではありますが、やはり楽しくイメージしたいもの。

そこで、今回は一風変わった、効果的なイメージを紹介します。

真分数・仮分数・帯分数の基本イメージ

まず真分数。

変形の余地がないので、真分数という言葉はあまり意識することがありません。忘れても大丈夫。

続いて仮分数。

あたまでっかちなイメージ。

これを帯分数にすると、

声に出すと、
「1と10分の7」

ということでしたね。

サイフ理論登場

さてさて、ここで、サイフをイメージしてください。

1を「お札」

お札が１枚と、小銭が７枚入っているサイフ
ということになります。

例題

基本のやり方はこうです。瞬時にできるとは思いますが、あえてスロー解説すると、

こんな感じでしょうか。ここで、サイフ理論登場！えっ、サイフ理論とは何ですかって？
「人間は、小銭よりお札が好き」

これがサイフ理論。

というのは、

小銭ジャラジャラのサイフ
なんですよ。

お店のレジを思い浮かべてください。前の人の商品が総て読み取られ、レジに540円と表示されます。そのお客は1000円札を出し、店員さんが「1000円お預かりします」と言ったその瞬間、
「40円あります！！」

この光景、だれしも一度は経験されているはず。果たして、そのお客さんはサイフの中をジャラジャラあさり、5秒、10秒…　このわずかな時間の長いこと。

人間って、そんなに小銭が嫌いなの？？

嫌いなんでしょうね。だって、もしここで40円を出さなければ、

460円もの小銭が返ってくる

→サイフの中はさらにジャラジャラになってしまう！じゃないですか。
人のことばかり言ってますが、自分も同じことをやりますよ。ただし、
先に40円を出してから、1000円札を出すようにしています。「同じだろ」って言われてしまいそうですが。

まとめ！サイフ理論

すなわち17枚の小銭のうち10枚は1枚のお札に両替できるので、
お札にして、札入れの部分に収納する

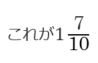
ということなのです。サイフがすっきりして満足できました。

ちょっと待てよ。
小銭だろうと、お札だろうと、
金額が同じなら、お金の本質って同じじゃない？
と思った方、鋭いです。
金額が同じなら、本質的に等しいことに気づいてしまったら、最早お札に両替することは意味を成しません。
そうです。小学校を卒業すると、帯分数表示は消えてしまうのでした。中学生になると、途端に仮分数表示に統一されてしまいますね。

こうして、物事の本質に気づくという事が、大人になるということであると、分数を通じて再認識することができました。
ジャラジャラを嫌って、小銭を目の敵にした私。でもそれは、お金を目の敵にしていたことになるのですね。反省します。

いかがでしたか。
こういうどうでもよさそうなことを考えることで、少しでもイメージが豊かになることを願っています。

続きはまたいつか。またお会いしましょう。