受験が近づいてまいりました。受験ドクターの安部公一郎です。

体調管理だけは万全に。

ここまでくると睡眠も勉強のうちです。

 

さて、

大好評だった、「円周率3的世界」

ご要望にお応えしてパート2です。

もちろん要望はきてないんですけど。

 

本日も3の話。

 

～前回の復習～

 

1）受験生にとっては、円周率が3だと、とても助かる！

↓

2）でも算数では困ることもある・・・

↓

3）3になりたい

 

シンプルな円周率3の世界。

もう一度、いってみよー。

 

〈こりゃ楽じゃ　いやむしろ便利〉

 

円周率が3だったら・・・

とにかく楽。

 

前回も言いました。

世の中生きていくのに、

大まかな数字さえわかれば問題なし！

 

赤道の長さをご存知ですか？

4万㎞。

 

じゃあ、

地球の直径は？

 

直径 × 円周率 ＝ 円周

 

ここで円周率3が登場。

 

直径 × 　　3　　　＝ 4万㎞

 

40000 ÷ 3 ＝ 13333

 

まぁ１万3000㎞くらい？

 

正解は、12742㎞。

 

だいたいOK！

 

どうですか。

40000÷3.14なんてやってられまへん。

40000÷3だからできるんです。

 

やっぱり円周率は3にすべきですね♪

 

〈いったいどこに行ったのだ〉

 

でもね、

算数では円周率3だと困ることもあるんですョ。

 

まだゆうか。

 

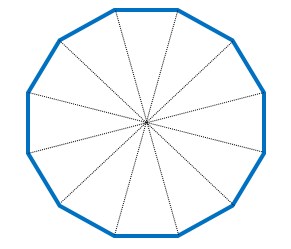
ここに正十二角形があります。

対角線の長さが、12ｃｍの正十二角形。

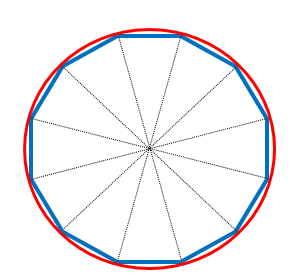
ここに直径12㎝の円があります。

 

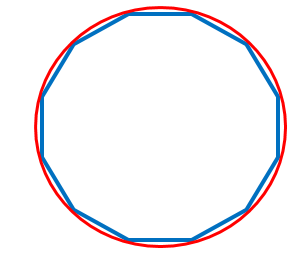
重ねてみると、こんな感じですね。

円の直径が12㎝ですから、

円の中に正十二角形がすっぽり。

 

すっぽり入るということは、

当然、正十二角形（青）が円（赤）より小さいことになります。

当たり前ですね。

 

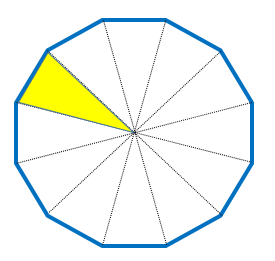
ここで、正十二角形の面積を求めてみましょう。

正十二角形は、

黄色い二等辺三角形12個で成り立ってますね。

 

黄色い二等辺三角形の面積を求めてみましょう。

 

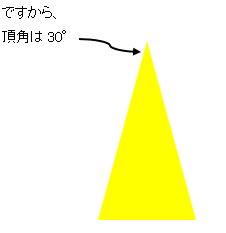
360° ÷ 12 ＝ 30°

 

中学受験生なら皆さん知っていますね。

30°ときたら、

30-60-90の直角三角形！

補助線を引いて、

30-60-90の直角三角形を作りましょう。

 

 

直角三角形ＡＢＣは、

30-60-90の直角三角形。

 

ＡＢが6ｃｍですから、ＢＣは3ｃｍですね。

 

黄色い二等辺三角形の面積は、

 

6 × 3 ÷ 2 ＝ 9㎠

 

それが12個ありますから、

正十二角形の面積は、

 

9 × 12 ＝ 108㎠

 

一方、円の面積はどうなりますか。

半径6ｃｍで、円周率が3、

 

6 × 6 × 3 ＝ 108㎠

 

どちらも108㎠・・・

 

なんじゃこぉりゃゃぁぁ・・・

 

正十二角形の面積と、円の面積が、

 

おぉんなじぃじゃゃぁぁ・・・

 

こんなことあっていいのでしょうか。

赤と青が同じ・・・

すみっこの空白はどこいった(´･ω･)?

 

やはり算数では、

円周率3は困りものですね。

 

ご納得いただけましたか。

 

〈祈！合格〉

 

たしかに円周率3では困る。

 

とはいえ、

ざっくり計算するときには便利です。

地球の直径もすぐに分かるし。

 

円周率3は日常生活で使え！

 

これが結論。

 

お手軽な3。

そんなフットワークのいい3を目標に、

皆さんも、受験乗り切って下さい。

祈！合格！

 

今宵はここまで。

ではまた。