みなさん、こんにちは！受験ドクター算数科のA.K講師です。

12月に入り、今年も残すところあと１か月。
突然ですが、私。最近、百人一首にはまっております。

ちはやぶる　神代もきかず　竜田川　からくれなゐに　水くくるとは　／　小倉百人一首17番　在原業平朝臣

皆さんはこの句をご存知でしょうか？

「たくさんの様々な不思議なことが起こっていたという神代の昔でさえも、こんなことは起こったことが未だにない。龍田川の水面に、埋め尽くされた紅葉が川の水をしぼり染めにしているとは。」
という意味です。なんと美しい一句なのでしょうか。
詠んだだけで、その景色が鮮やかに頭に浮かんできませんか？
この「竜田川」とは、奈良県斑鳩町に実際にある地名です。紅葉の有名な名所らしいので、ぜひ皆さんも興味がおありでしたら訪れてみてください。

今日の前置きはここまで。
本題に参りましょう。今回のテーマは、俳句に紹介された竜田川…川の水面…水…そう、食塩水！(笑)を扱っていきます。
入試で避けては通れない単元の一つである、割合！
その中でも、食塩水について今日はスポットライトを当てていこうと思います。
濃度の違う食塩水同士を混ぜ合わせる場合には、いくつかの考え方が存在します。

【問題１】
3％の食塩水300gと、10％の食塩水400gを混ぜると、濃度は何％になりますか。

①塩の量を、食塩水の全体量と濃度から一つずつ求める！
3％の食塩水300g ⇒ 含まれる塩の量は300×0.03=9g
10％の食塩水400g ⇒ 含まれる塩の量は400×0.1=40g
混ぜ合わせると、塩の量は9+40=49g、全体の量は300+400=700g。
よって、49÷700=0.07なので7％

ところが！この方法ではうまくいかない問題も世の中には存在するのです…。

【問題２】
10％の食塩水と、21％の食塩水を混ぜると、13％の食塩水が550gできました。何gずつ混ぜましたか。

ん？あれっ…それぞれの全体量が分からないと、塩の量が分からないじゃないか！
その通り。塩の量を考えるのではなく、別のアプローチが必要になります。

②食塩水の面積図を描き、平均算としてとらえる！
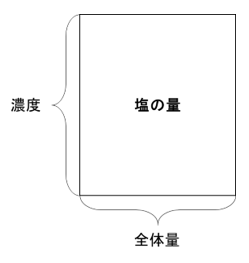
本日、お伝えしたいのがこの内容です。食塩水の全体量、濃度、塩の量は以下のような図で関係を表せます。

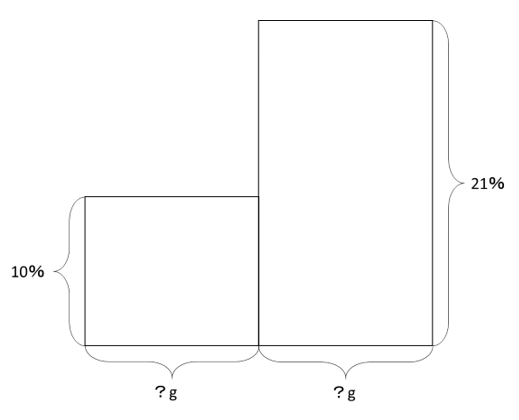
問題の情況を、この図にしてみると以下のように2つの長方形が出来ますね。

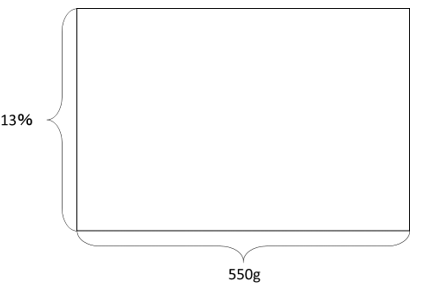
混ぜ合わせた後の状態は、以下のようになります。

では…ここで２つの図を、重ね合わせてみましょう！

高さを揃えたので、右側の長方形の出っ張っている赤い部分が左側の長方形のへこんでいる青い部分に移ったことになり、２つの面積は一緒です。
赤い長方形の縦は21-13=8、青い長方形の縦は13-10=3。比にすると8:3です。各々の長方形の面積は同じですから、横の長さは逆比になります。よって、赤い長方形の横：青い長方形の横＝3:8。よって、③+⑧=⑪gが550gとなりますので、比例配分で10%の食塩水が400g、21%の食塩水が150gとなるわけです！！

この面積図、大変便利なのです…。3種類の食塩水を混ぜ合わせる場合も、有効ですよ。

【問題３】
5％の食塩水100gと、8％の食塩水と、10%の食塩水300gを混ぜると、濃度が8.5％になりました。8%の食塩水を何g混ぜましたか。

塩の量が求まらないので、面積図を使ってみます。

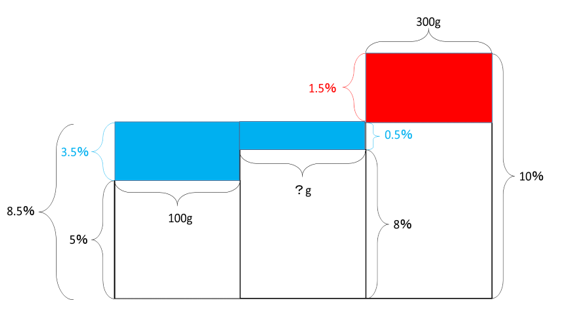
今回は、赤い長方形の面積と青い2つの長方形の面積の和が等しくなりますね。
赤：300×1.5=450、左青：100×3.5=350となるので、右青は450-350=100となります。
よって、8％の食塩水は100÷0.5=200gと分かるわけです。
（なお、今回は長方形が全部で3つあるので、先ほどの問題のような逆比は使えないので注意！）

本日の内容、いかがでしたか？この辺で今日のまとめとしましょう。

～本日のまとめ～
①濃度の違う食塩水の混合問題では、まずは塩の量に着目。
②全体量が分からないために塩の量が出せない場合は、面積図を描いてみる。
③3種類の食塩水を混ぜた場合も、面積図は有効。ただし、逆比ではなく面積を求めて考える。

では今日はここまで。
今回も長々とお付き合いいただき、ありがとうございました。
次回は…今回の続きとして、食塩水のちょっと難しめな入試問題を皆様に挑戦していただきます。

それでは。次回も、お楽しみに！！