みなさん、こんにちは。
算数・理科講師のM.Sです。

本日は、正六角形についてお話をしたいと思います。
正六角形はコツをつかむと得点しやすいと思いますので、まだ未修得の人は練習していきましょう。

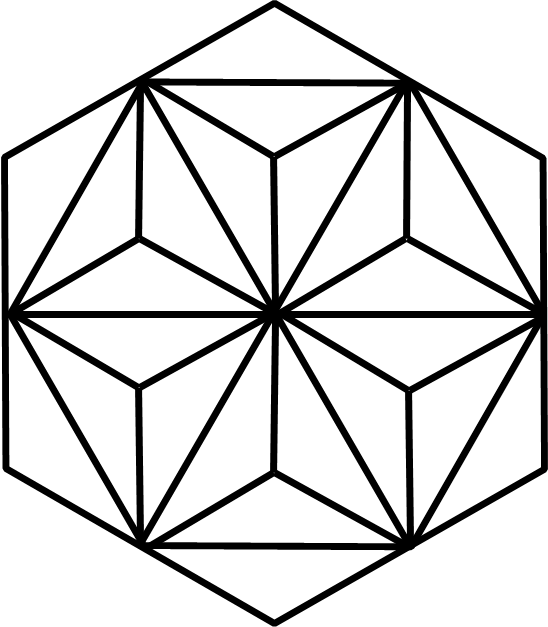
まずは、基本の正六角形を6分割した図を覚えましょう。
★　正三角形

★　二等辺三角形

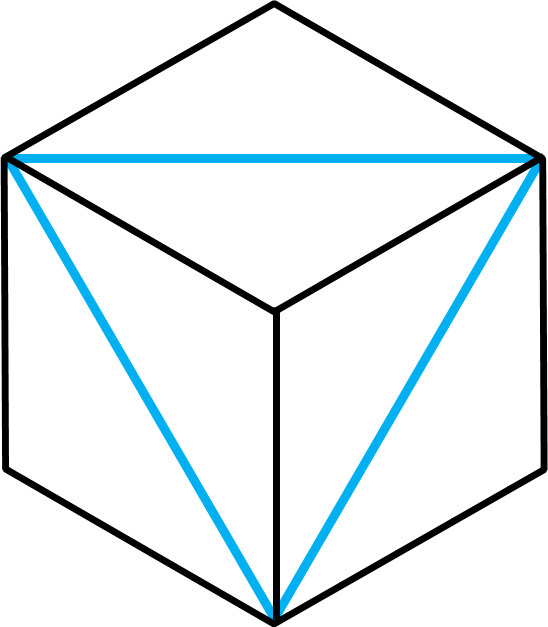
次に、上の6分割を組み合わせた12分割した図も覚えましょう。

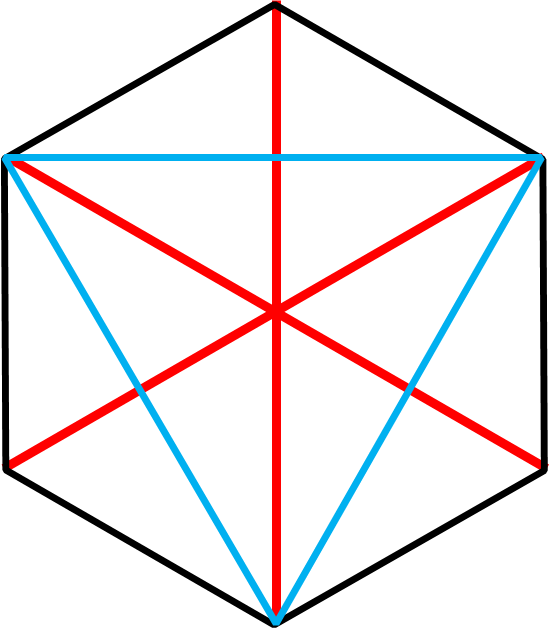
そして、これもマスターすると便利な18分割した図です。
　　　

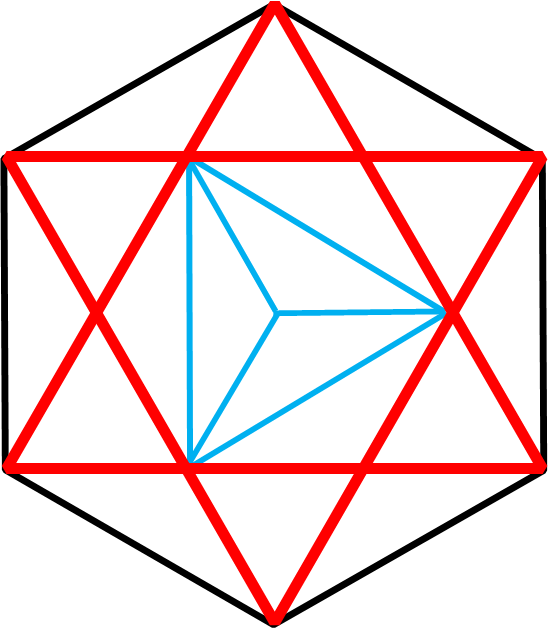
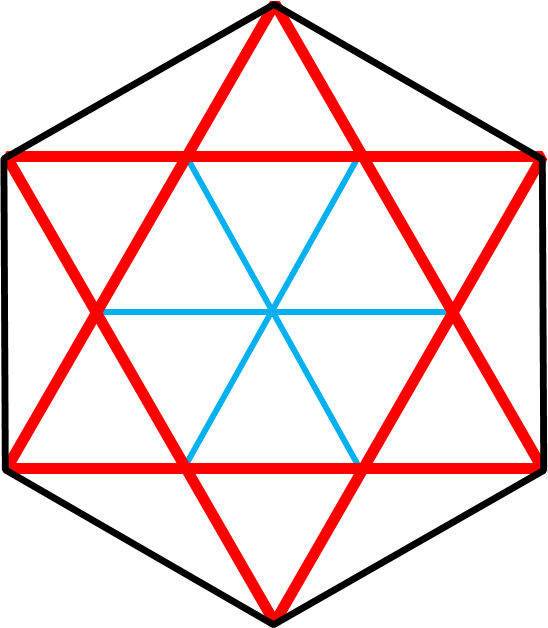
最後に、ここまで習得すれば完璧の24分割した図です。
★　二等辺三角形

では、問題に取り組んでみましょう。

問題
次の斜線部分の面積は、正六角形の面積の何倍ですか。
①　　　　　②

①は24分割の図を使います。
18÷24＝倍＝0.75倍
②は図のように18分割にすれば簡単です。

４÷18＝倍
また、②は比を使って解くこともできます。
△ABGと△CFGは相似で、
AG：GC＝AB：CF＝1：2
これから、双子山より、
×＝倍

正六角形の問題は、分割の図や『Aをねらえ』や『双子山』などを組み合わせた問題が多くありますので、しっかりと練習していきましょう。

問題
六角形ABCDEFは正六角形です。AM：BM=1：1，CN：ND=1：2とき、四角形BCNMは正六角形ABCDEFの何倍ですか。

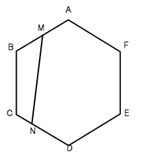
図のように、補助線を引きます。

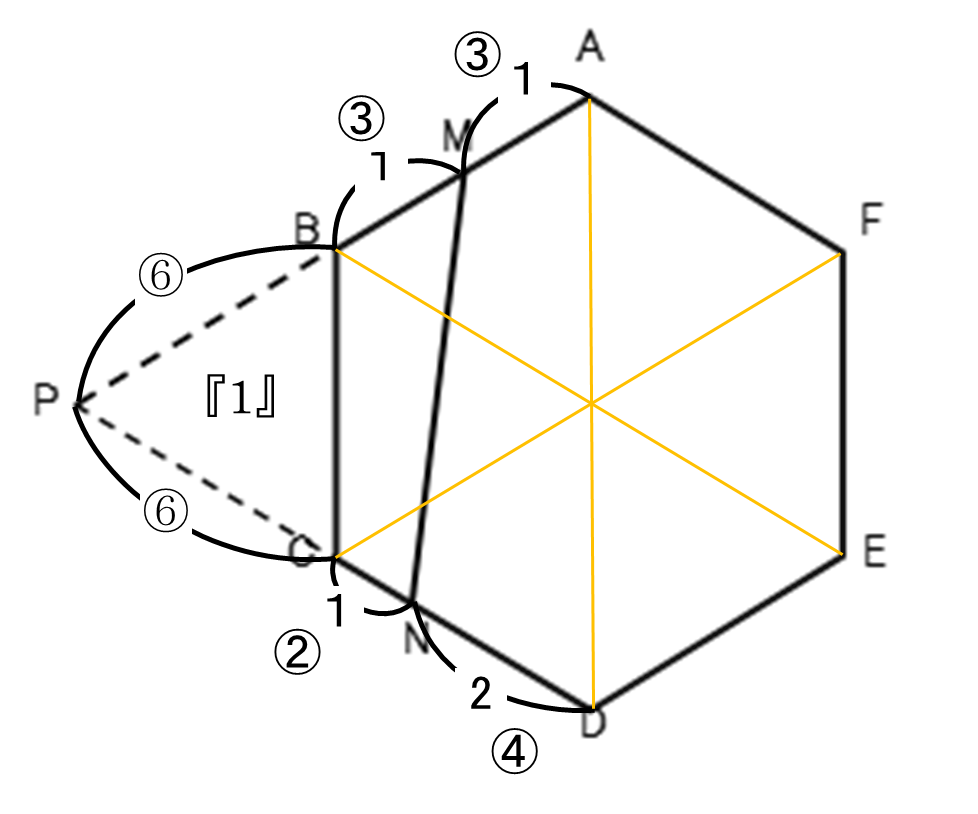
正六角形ABCDEFの面積を『６』とすると、
三角形PNMの面積＝『４』×
＝『４』× ＝『２』
四角形BCNM＝『２』－『１』＝『１』
よって、
『１』÷『６』＝倍

★　補助線を引いて、正三角形をつけたす発想はよく使います。正五角形でも見かけたりするので、覚えておいてくださいね。

最後に、正六角形ではないですが、頻出問題を紹介します。

問題
６つの角がすべて120°の六角形ABCDEFがあり、辺の長さは図のようになっています。この六角形の面積は１辺の長さが1cmの正六角形の面積の何倍ですか。

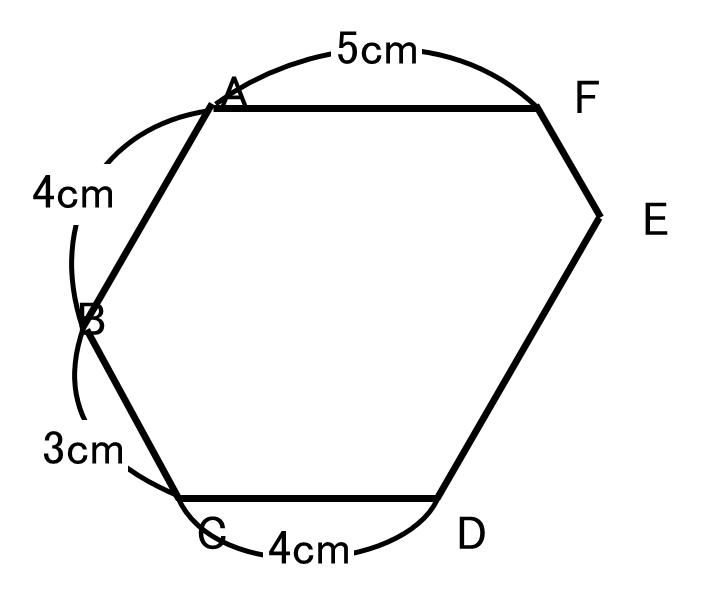
この問題は、問題文の『６つの角がすべて120°(もしくは等しい)の六角形・・・』を見たときに，大きな正三角形で囲むことを思い出せるようにしましょう。

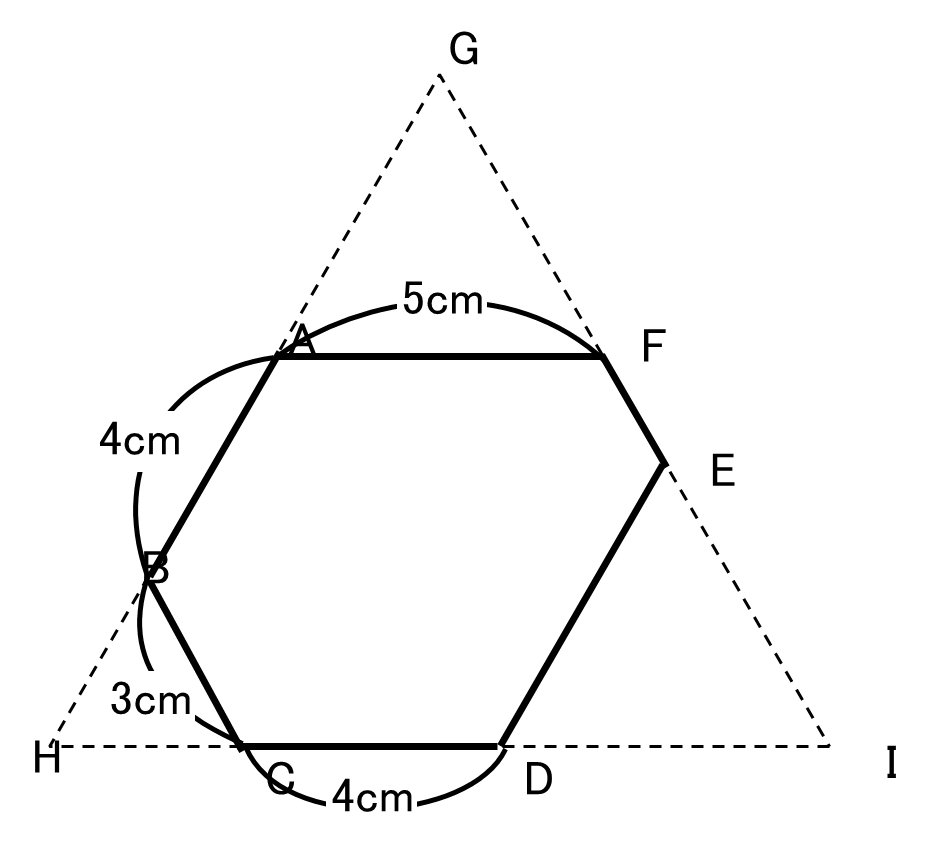
六角形ABCDFEの外角は60°から、
右の図のように、正三角形で囲むと、正三角形GHIの
1辺の長さは12cmです。

1辺の長さが1cmの正六角形の面積の『６』とすると、
1辺の長さが1cmの正三角形の面積は『１』です。

六角形ABCDEFの面積
＝△GHI－(△GAF＋△BHC＋△EDI)
＝『12×12』－(『5×5』＋『3×3』＋『5×5』)
＝『144』－(『25』＋『9』＋『25』)
＝『144』－『59』＝『85』
よって、
『85』÷『６』＝倍

六角形の問題で、使う道具(武器)は限られているので、特に、Aをねらえの使い方は、五角形などにも応用できるようにしておきましょう。