みなさん、こんにちは。受験ドクターの安部公一郎です。

 

台風連発です。

こんなに雨が降ると、東京タワーが心配ですね。

水没するんじゃなかろうか。

東京タワーとスカイツリー。

ご存知 333mと634m。

 

高さの平均は何メートルですか？

 

カンタンだよ！

 

（ 333 + 634 ） ÷ 2 = 483.5m

 

正解。

 

平均なんてカンタンだよ！

 

いやいや、

はたしてそうでしょうか。

 

・平均の根本原理その1　『平均は量の多い方に引っ張られる』

・平均の根本原理その2　『比率が変わらなければ、平均も変わらない』

 

ここをきちんと理解する必要があります。

どうですか？

〈平均は量の多い方に引っ張られる〉

 

平均は量の多い方に引っ張られる…

ナニソレ。

 

いま、

1個100円のリンゴと、1個50円のミカンがあるとしましょう。

 

以下のような買い方をした場合、

1個当たりの平均は何円ですか？

 

 

全部リンゴの場合は、

もちろん平均は100円ですね。

100円ばっかりですから。

 

全部ミカンの場合も、

もちろん平均は50円ですね。

50円ばっかりですから。

 

当たり前です。

 

でも、

 

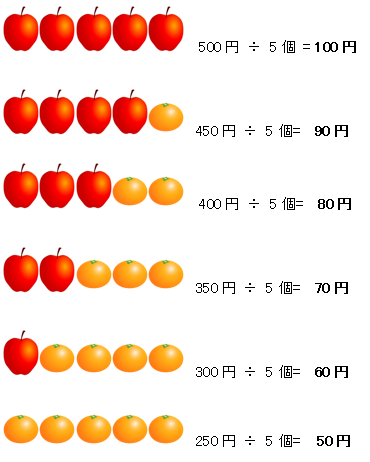
リンゴ4個・ミカン1個のときは、90円

リンゴ3個・ミカン2個のときは、80円

リンゴ2個・ミカン3個のときは、70円

リンゴ1個・ミカン4個のときは、60円

 

平均は変化していきますね。

 

どのように変化してますか？

 

そうです！

量の多い方に引っ張られていくんですぅ！

 

リンゴが多いと、

平均はリンゴの値段の100円に近くなります。

ミカンが多いと、

平均はミカンの値段の50円に近くなります。

 

平均は常に同じではなく、

量が多い方に近づいていくのです。

 

10円玉の方が多いですねぇ。

ということは、

 

平均は、（ 10 + 50 ） ÷ 2 = 30円より、

10円に近いはずです。

 

やってみましょう。

 

（ 10 × 7 +  50 × 3 ） ÷ 10 = 22円

 

どうですか。

10円に近づいてますね。

 

平均の根本原理その1　『平均は量の多い方に引っ張られる』

クリア！

 

 

〈比率が変わらなければ、平均も変わらない〉

 

比率が変わらなければ、平均も変わらない…

ナニソレ。

 

ここでまたリンゴとミカンに登場してもらいましょう。

 

350円 ÷ 5個 =  70円

 

リンゴもミカンも2倍の

リンゴが4個、ミカンが6個だと、

どうでしょう。

100円 × 4個 + 50円 × 6個 ＝ 700円

700円 ÷ 10個 ＝ 70円

 

どちらも70円です。

一緒ですね。

 

そうです。

全体量が変化しても、

比率が変わらなければ、

平均は変わらないのです。

 

 

平均の速さとは、

「進んだ距離の合計÷かかった時間の合計」で求められます。

 

600m ÷ 40 ＝ 15分

600m ÷ 60 ＝ 10分

（ 600m + 600m ） ÷ （ 15分 + 10分 ） ＝ 48m …往復の平均の速さ

 

ここで距離を600mから1800mにしてみましょう。

 

 

1800m ÷ 40 ＝ 45分

1800m ÷ 60 ＝ 30分

（ 1800m + 1800m ） ÷ （ 45分 + 30分 ） ＝ 48m …往復の平均の速さ

 

どちらも分速48mです。

一緒ですね。

 

距離が変わっても、

分速40mで歩いている時間と

分速60mで歩いている時間の比率が変化していないので、

往復の平均の速さは同じです。

 

平均の根本原理その2　『比率が変わらなければ、平均も変わらない』

クリア！

 

〈華麗なるヘイキン〉

 

さて、本日のまとめ。

 

・平均の根本原理その1　『平均は量の多い方に引っ張られる』

・平均の根本原理その2　『比率が変わらなければ、平均も変わらない』

 

このふたつを理解すれば、

平均はOK。

 

みなさんは理解しましたね♪

もはや平均的な中学受験生を上回ったと申せましょう。

平均を味方につけて

算数を攻略しよう‼

 

今宵はここまで。

ではまた。