こんにちは！算数科のEです。

 

6年生の皆さん、先日行われた第１回合不合判定テストはいかがでしたか？

 

計6回にわたって行われるこのテストは、回数を繰り返してテストに慣れる、とか

回数を増やしてデータの信ぴょう性を高めるという意図の他に、

6年生の全範囲にわたって出題する、ということを目指しています。

四谷大塚の公式サイトにもあるように、

1回のテストで出題することができる学習領域には限りがあるため、

6回のテスト機会を設けることで、受験に必要な領域をできるだけ網羅して出題する、

というコンセプトで作成されています。

 

したがって点数や偏差値で一喜一憂しておしまいにせず、

しっかりと振り返り分析しておくことが重要です。

どんなテーマが正解できて、何がまだ曖昧だったのか。

自分自身の「解ける問題だ」という見極めや、「解けた」という手ごたえは、

実際の正答状況と一致していたかどうか。

最低限、以上の2点を意識して、振り返っておきましょう。

 

【2016年度第1回合不合判定テスト出題テーマ】

ちなみに算数の第1回で出題されたテーマは以下の通りです。

2⃣

(1)仕事算

(2)周期算

(3)柱体の表面積

(4)組み合わせ(リーグ戦)

(6)おうぎ形の面積

3⃣

池の周りの旅人算

4⃣

倍数と集合

5⃣

平面図形と比

6⃣

(1)折り返し(角度)

(2)比と割合の文章題

(3)3量のつるかめ算

7⃣

個数のある売買

8⃣

体積と底面積・高さの関係

(おもりを沈める問題)

9⃣

規則性の利用

 

算数が苦手なお子さんでも、4⃣の(1)までは確実に得点できる状態に

しておきたいところです。

 

また、頻出テーマであるにもかかわらず、今回出題されなかった、

食塩水の問題や過不足算、円すいに関する問題などは、次回7月10日の

第2回合不合判定テストで問われる可能性が高いですね。

しっかり対策を練って臨みましょう。

四谷大塚・早稲田アカデミー生のための偏差値20アップ学習法はこちら！
http://www.chugakujuken.com/hensa20up/j_betsu/j_yotsuya/

【注目の1題　規則性を図で視る】

さて、今回のブログでは9⃣で出題された「規則性」の応用問題を、

目に見えるように図にしてみましょう。

 

問題ではこのような数の並びが示されていました。

1

1  2

1  3  5

1  4  7  10

 

どの段の数字も1から「始まり」ますが、

下の段に行くにつれて、並ぶ数字の「個数」が

1段目→1個

2段目→2個

3段目→3個

4段目→4個

と、だんだん増えながら、

 

並ぶ「数どうしの隔たり」は

2段目→隣の数との差が1

3段目→隣の数との差が2

4段目→隣の数との差が3

と、だんだん広がっています。

 

ここまで分析しただけでも、(1)なら解ける可能性がありますね。

 

100段目の右端は

１から「始まり」

100「個」並んでおり

隣の数との「差」は99ですから、

等差数列のＮ番目を求める公式に当てはめて

1＋99×（100−1）＝9802

と、求めることができました。

 

では(2)はどうでしょうか？

この数の並びの中で、1回しか現れない数にフォーカスを当て、

1回しか現れない数のうち小さい方から数えて10番目の数は何かと聞かれています。

 

決まりはシンプルですが、この先どんな数が現れてくるのか？

現れない数に何かしら決まりはあるのか？

 

一見、むむむっ、となるかもしれません。

それぞれの段に登場する数字を全部書き出して、

根性でチェックするしかないのでしょうか。

書き出す時間の余裕や気力が残っていればそれもありですが、

何か仕掛けがあるんじゃないか、気になるところですね。

 

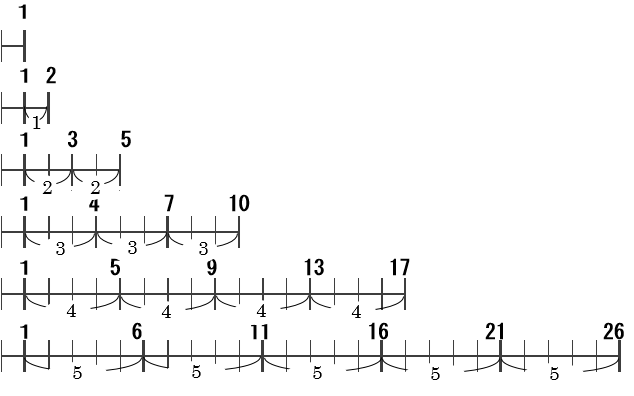
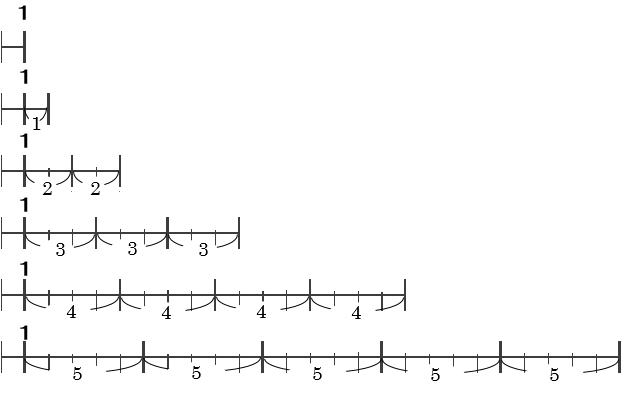
ところで、これらの数の並びを数直線でイメージしてみるとどうなるでしょうか？

これを、はじめの「１」までと、そこから先とに分けてから、「１」より先の部分に注目してみます。

そろっている「１」のところをスタート地点（０）のようにして考えてみると、

2段目の1

3段目の2

4段目の3

6段目の5

は、これ以外に縦に一致する点が存在しません。

一方で、4は5段目にも3段目にも登場します。

 

このように、一致するものがあるかないかを決定づける要素は何でしょうか。

それは、スタート地点からの隔たりを、複数の表し方ができるか、

それとも一通りの表し方しかできないか、という違いですね。

1や2や3や5では、それ以外の表し方ができないので、他のどの段とも重複しません。

4の場合は、2×2と4×１という2種類の表し方が存在します。

 

つまり、他の数のかけ算の形で表せない数、すなわち「素数（または１）」が初めに登場する点では、

他のどの段とも重複しない、という法則が発見できました。

 

したがって、小さい方から1、2、3、5、7、11、13、17、19、23で、10番目は23になります。

実際に登場する数としては、初めに切り離していた1を加えて

23＋1＝24ということになります。

 

続く(3)では111が現れる段が問われています。

同じように考えてみると、

111−1＝110を作ることができるのは何の倍数か？ということになります。

110は何の倍数かというと、約数を書き出してみれば、2、5、10、11、22、55、110ですね。

 

2の倍数は3段目ですが、110まで至りません

5の倍数は6段目ですが、110まで至りません。

10の倍数は11段目ですが、これも110までは至りません（10×10＝100まで）

11の倍数は12段目で、数が12個ならびますので、11×10＝110が登場します。

22の倍数は23段目でＯＫ

55の倍数は56段目でＯＫ

110の倍数は111段目でＯＫです。

 

よって、12、23、56、111段目が当てはまり、それ以外にはないということもわかります。

 

【今回のまとめ】

このように、数が登場した時に、視覚化することによって、

「分ける」ポイントが発見しやすくなったり

「ボリューム感」を感じながらアプローチしていくことで、

ひらめきが浮かびやすくなる効果があります。

大きな数は長い線で。広い隔たりは遠く離れた点として、

目で見て数を感じて、複雑な問題に隠された

シンプルなトリックを見抜いていきましょう。